Chứng minh biểu thức sau không phụ thuộc vào x:
A = 1 sin 4 x + 1 sin 8 x + 1 sin 16 x - c o t 2 x + c o t 16 x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
18 tháng 8 2019
Đúng(0)
Những câu hỏi liên quan
12 tháng 6 2023
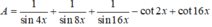
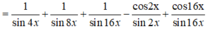
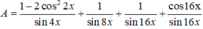
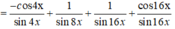
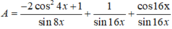
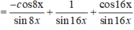
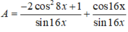
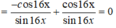
Sửa đề: sin^4x+cos^4x+1
\(A=\dfrac{\left(sin^2x+cos^2x\right)^3-3sin^2xcos^2x+2}{\left(sin^2x+cos^2x\right)^2-2sin^2xcos^2x+1}\)
\(=\dfrac{3\left(1-sin^2xcos^2x\right)}{2\left(1-sin^2xcos^2x\right)}=\dfrac{3}{2}\)
5 tháng 7 2021
1,\(A=3\left(sin^4x+cos^4x\right)-2\left(sin^2x+cos^2x\right)\left(sin^4x-sin^2x.cos^2x+cos^4x\right)\)
\(=3\left(sin^4x+cos^4x\right)-2\left(sin^4x-sin^2x.cos^4x+cos^4x\right)\)
\(=sin^4x+2sin^2x.cos^2x+cos^4x=\left(sin^2x+cos^2x\right)^2=1\)
Vậy...
2,\(B=cos^6x+2sin^4x\left(1-sin^2x\right)+3\left(1-cos^2x\right)cos^4x+sin^4x\)
\(=-2cos^6x+3sin^4x-2sin^6x+3cos^4x\)
\(=-2\left(sin^2x+cos^2x\right)\left(sin^4x-sin^2x.cos^2x+cos^4x\right)+3\left(cos^4x+sin^4x\right)\)
\(=-2\left(sin^4x-sin^2x.cos^2x+cos^4x\right)+3\left(cos^4x+sin^4x\right)\)\(=cos^4x+sin^4x+2sin^2x.cos^2x=1\)
Vậy...
3,\(C=\dfrac{1}{2}\left[cos\left(-\dfrac{7\pi}{12}\right)+cos\left(2x-\dfrac{\pi}{12}\right)\right]+\dfrac{1}{2}\left[cos\left(-\dfrac{7\pi}{12}\right)+cos\left(2x+\dfrac{11\pi}{12}\right)\right]\)
\(=cos\left(-\dfrac{7\pi}{12}\right)+\dfrac{1}{2}\left[cos\left(2x-\dfrac{\pi}{12}\right)+cos\left(2x+\dfrac{11\pi}{12}\right)\right]\)\(=\dfrac{-\sqrt{6}+\sqrt{2}}{4}+\dfrac{1}{2}\left[cos\left(2x-\dfrac{\pi}{12}\right)+cos\left(2x-\dfrac{\pi}{12}+\pi\right)\right]\)
\(=\dfrac{-\sqrt{6}+\sqrt{2}}{4}+\dfrac{1}{2}\left[cos\left(2x-\dfrac{\pi}{12}\right)-cos\left(2x-\dfrac{\pi}{12}\right)\right]\)\(=\dfrac{-\sqrt{6}+\sqrt{2}}{4}\)
Vậy...
4, \(D=cos^2x+\left(-\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx\right)^2+\left(-\dfrac{1}{2}.cosx+\dfrac{\sqrt{3}}{2}.sinx\right)^2\)
\(=cos^2x+\dfrac{1}{4}cos^2x+\dfrac{\sqrt{3}}{4}cosx.sinx+\dfrac{3}{4}sin^2x+\dfrac{1}{4}cos^2x-\dfrac{\sqrt{3}}{4}cosx.sinx+\dfrac{3}{4}sin^2x\)
\(=\dfrac{3}{2}\left(cos^2x+sin^2x\right)=\dfrac{3}{2}\)
Vậy...
5, Xem lại đề
6,\(F=-cosx+cosx-tan\left(\dfrac{\pi}{2}+x\right).cot\left(\pi+\dfrac{\pi}{2}-x\right)\)
\(=tan\left(\pi-\dfrac{\pi}{2}-x\right).cot\left(\dfrac{\pi}{2}-x\right)\)\(=tan\left(\dfrac{\pi}{2}-x\right).cot\left(\dfrac{\pi}{2}-x\right)\)\(=cotx.tanx=1\)
Vậy...
28 tháng 7 2023
b: \(B=sin^2x\left(sin^2x+cos^2x\right)+cos^2x\)
\(=sin^2x+cos^2x=1\)
c: \(=cos^2x\left(cos^2x+sin^2x\right)+cos^2x\)
=cos^2x+cos^2x
=2*cos^2x có phụ thuộc vào x nha bạn
AH
Akai Haruma
Giáo viên
13 tháng 8 2018
Lời giải:
a) Ta có tính chất quen thuộc là nếu \(\alpha+\beta=90^0\Rightarrow \cos \alpha=\sin \beta\)(có thể thấy rất rõ khi xét một tam giác vuông)
Tức là \(\sin \beta=\cos (90-\beta)\)
Do đó:
\(A=(\sin ^22^0+\sin ^288^0)+(\sin ^24^0+\sin ^286^0)+...+(\sin ^244^0+\sin ^246^0)\)
\(=\underbrace{(\sin ^22^0+\cos ^22^0)+(\sin ^24^0+\cos ^24^0)+...+(\sin ^244^0+\cos ^244^0)}_{22\text{cặp}}\)
\(=\underbrace{1+1+...+1}_{22}=22\) (tổng 2 bình phương sin và cos của một góc thì bằng 1)
b)
\(P=1994(\sin ^6x+\cos ^6x)-2991(\sin ^4x+\cos ^4x)\)
\(=1994[(\sin ^2x+\cos ^2x)(\sin ^4x-\sin ^2x\cos^2 x+\cos ^4x)]-2991(\sin ^4x+\cos ^4x)\)
\(=1994(\sin ^4x-\sin ^2x\cos ^2x+\cos ^4x)-2991(\sin ^4x+\cos ^4x)\)
\(=-1994\sin ^2x\cos ^2x-997\sin ^4x-997\cos ^4x\)
\(=-997(\sin ^4x+2\sin ^2x\cos ^2x+\cos ^4x) \)
\(=-997(\sin ^2x+\cos ^2x)^2=-997\)
Do đó biểu thức không phụ thuộc vào $x$
TN
19 tháng 5 2016
mình ghi đáp án cho cái lượng giác này thui nhé
\(=\frac{3}{2}\)
TN
19 tháng 5 2016
A=sin2x+sin2x\(\left(\frac{2\pi}{3}+x\right)\)+sin2\(\left(\frac{2\pi}{3}-x\right)\)
\(A=\sin^2x+\left[\sin\left(\frac{2\pi}{3}+x\right)+\sin\left(\frac{2\pi}{3}-x\right)\right]^2-2\sin\left(\frac{2\pi}{3}-x\right).\sin\frac{2\pi}{3}+x\)
\(A=\sin^2x+4\left[\frac{\sin2\pi}{3}.\sin x\right]^2-\left[\frac{\sin4\pi}{3}+\sin2x\right]\)
\(A=\sin^2x+\sin x^2-\left[\sin2x-\frac{1}{2}\right]\)
\(A=2\sin x^2-\left[2\sin^2x-\frac{3}{2}\right]\)
\(A=\frac{3}{2}\)
vậy biểu thức trên ko phụ thuộc vào biến số x
AT
30 tháng 7 2021
\(\left(\sqrt{\dfrac{1+sin\alpha}{1-sin\alpha}}+\sqrt{\dfrac{1-sin\alpha}{1+sin\alpha}}\right).\dfrac{1}{\sqrt{1+tan^2\alpha}}\)
\(=\left(\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{\left(1-sin\alpha\right)\left(1+sin\alpha\right)}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{\left(1+sin\alpha\right)\left(1-sin\alpha\right)}}\right).\dfrac{1}{\sqrt{1+\left(\dfrac{sin\alpha}{cos\alpha}\right)^2}}\)
\(=\left(\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{1-sin^2\alpha}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{1-sin^2\alpha}}\right).\dfrac{1}{\sqrt{\dfrac{cos^2\alpha+sin^2\alpha}{cos^2\alpha}}}\)
\(=\left(\sqrt{\dfrac{\left(1+sin\alpha\right)^2}{cos^2\alpha}}+\sqrt{\dfrac{\left(1-sin\alpha\right)^2}{cos^2\alpha}}\right).\dfrac{1}{\sqrt{\dfrac{1}{cos^2\alpha}}}\)
\(=\left(\dfrac{1+sin\alpha}{cos\alpha}+\dfrac{1-sin\alpha}{cos\alpha}\right).\dfrac{1}{\dfrac{1}{cos\alpha}}=\dfrac{2}{cos\alpha}.cos\alpha=2\)
BH
27 tháng 7 2019
1) \(\frac{1-2\sin\alpha\cdot\cos\alpha}{sin^2\alpha-\cos^2\alpha}=\frac{sin^2\alpha+\cos^2\alpha-2sin\alpha\cdot\cos\alpha}{sin^2\alpha-\cos^2\alpha}\)\(=\frac{\left(sin\alpha-\cos\alpha\right)^2}{sin^2\alpha-\cos^2\alpha}=\frac{sin\alpha-\cos\alpha}{sin\alpha+\cos\alpha}\)(đpcm)
2) \(cos^4\alpha+sin^2\alpha\cdot cos^2\alpha+sin^2\alpha\)
\(=cos^4\alpha+\left(1-cos^2\alpha\right)\cdot cos^2\alpha+sin^2\alpha\)
\(=cos^4\alpha+cos^2\alpha-cos^4\alpha+sin^2\alpha\)
\(=cos^2\alpha+sin^2\alpha=1\)(đpcm)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 6 2020
\(B=cos^2x.cot^2x+cos^2x-cot^2x+2\left(sin^2x+cos^2x\right)\)
\(=cos^2x\left(cot^2x+1\right)-cot^2x+2\)
\(=\frac{cos^2x}{sin^2x}-cot^2x+1=cot^2x-cot^2x+1=1\)
\(M=cos^4x-sin^4x+cos^4x+sin^2x.cos^2x+3sin^2x\)
\(=\left(cos^2x-sin^2x\right)\left(cos^2x+sin^2x\right)+cos^2x\left(cos^2x+sin^2x\right)+3sin^2x\)
\(=cos^2x-sin^2x+cos^2x+3sin^2x\)
\(=2\left(sin^2x+cos^2x\right)=2\)