Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đường tròn (C1): x2+ y2 – 4= 0 có tâm O(0; 0) bán kính R= 2;
Đường tròn (C2) ( x -8) 2+ (y- 6)2= 4 có tâm I( 8; 6) bán kính R= 2.
Mà OI = 8 2 + 6 2 = 10
Ta thấy: OI> 2+2 nên 2 đường tròn đã cho không cắt nhau.
Chọn A.
Ta có: (C1): x2+ y2 – 4 = 0 có tâm O (0; 0) và bán kính R= 2;
Dường tròn (C2): (x-3)2+ (y-4) 2= 25 có tâm I( 3;4) và R= 5 nên OI= 5
Ta thấy: 5-2 < OI< 5+ 2
nên chúng cắt nhau.
Chọn B.
Đáp án A
- Từ giả thiết : đường tròn (C1) tâm I(0;0); R = 13 đường tròn (C2) tâm J( 6;0) và R’= 5
- Gọi đường thẳng d qua A có véc tơ chỉ phương:
- d cắt (C1) tại A,B:
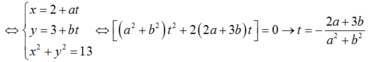
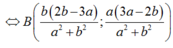
Tương tự d cắt (C2) tại A; C thì tọa độ của A; C là nghiệm của hệ :
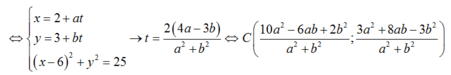
- Nếu 2 dây cung bằng nhau thì A là trung điểm của A; C .Từ đó ta có phương trình :
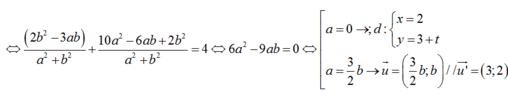
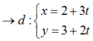
Vậy có 2 đường thẳng: d: x-2 = 0 và d’: 2x -3y + 5= 0.
Đường tròn (C1) có tâm và bán kính: I1=(0;0), và R1= 2; (C2) có tâm I2 (-10; 16) và bán kính R2= 1; khoảng cách giữa hai tâm .
Vậy 2 đường tròn đã cho không có điểm chung.
Chọn B.