Với giá trị nào của m hai đường thẳng sau đây vuông góc nhau ?
∆1 : mx+ y-19 = 0 và ∆2 : (m-1) x+ (m+1) y-20 = 0
A. Mọi m.
B.m= 1
C. Không có m.
D. m= -1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Để hai đường thẳng trùng nhau thì trước tiên ta có: \(\frac{1}{m}=\frac{-m}{-1}=m(m\neq 0)\Leftrightarrow m=\pm 1\)
Nếu $m=1$ thì $(d_1): x-y=0$ và $(d_2): x-y=2$ không trùng nhau được
Nếu $m=-1$ thì $(d_1): x+y=0$ và $(d_2): x+y=0$ trùng nhau
Đáp án D.

Vecto pháp tuyến của là: \(\overrightarrow {{n_1}} = \left( {m; - 1} \right)\)
Vecto pháp tuyến của là: \(\overrightarrow {{n_2}} = \left( {2; - 1} \right)\)
Vậy ai đường thẳng \({\Delta _1}\),\({\Delta _2}\) vuông góc với nhau khi và chỉ khỉ \(\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} \) vuông góc với nhau tức là \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 0 \Leftrightarrow 2m + 1 = 0 \Leftrightarrow m = \frac{{ - 1}}{2}\)

Giải
Đường thẳng( d1 ) : y = -mx + m + 1 có a1 = -m
Đường thẳng ( d2 ) : y =\(\frac{1}{m}x-1-\frac{5}{m}\)có a2 = \(\frac{1}{m}\)
Ta có : a1.a2 = ( -m ) . \(\frac{1}{m}\)=-1 .Vậy ( d1 ) và ( d2 ) vuông góc với nhau với mọi giá trị của tham số m khác 0 => đpcm

+ Hai đường thẳng cắt nhau tại một điểm trên trục hoành suy ra tung độ giao điểm là y=0.
+ Từ đây ta có: (m-1)x-5=9 suy ra 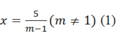
Đồng thời: mx+7=0 suy ra x= -7/m ( m≠0) (2)
+ Từ (1) và (2) ta có: 
Chọn D.

(d): VTPT là (m;1)
(d'): VTPT là (m;-4)
(d) vuông góc (d')
=>m^2-4=0
=>m=2 hoặc m=-2
=>Có 2 số nguyên m thỏa mãn
Đường thẳng Δ1 có vectơ pháp tuyến là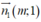 .
.
Đường thẳng Δ2 có vectơ pháp tuyến là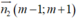 .
.
Hai đường thẳng vuông góc khi và chỉ khi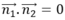
Suy ra : m( m-1) + m+ 1= 0 hay m2+1 = 0 phương trình vô nghiệm.
Vậy không có giá trị của m để hai đường thẳng vuông góc.
Chọn C.