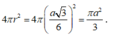Cho tam giác đều ABC cạnh a. Gọi (P) là mặt phẳng chứa BC và vuông góc với mặt phẳng (ABC). Trong (P), xét đường tròn (C) đường kính BC. Diện tích mặt cầu nội tiếp hình nón có đáy là (C), đỉnh là A bằng
A . πa 2 2
B . πa 2 3
C . πa 2
D . 2 πa 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

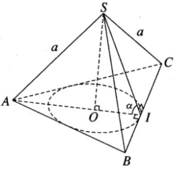
Gọi I là trung điểm của cạnh BC và O là tâm của tam giác đều ABC. Theo giả thiết ta có SA = SB = SC = a và ∠ SIO = α. Đặt OI = r, SO = h, ta có AO = 2r và

Do đó a 2 = r 2 tan 2 α + 4 r 2 = r 2 tan 2 α + 4
Vậy 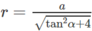
Hình nón nội tiếp có đường sinh là :
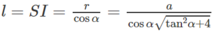
Diện tích xung quanh của hình nón nội tiếp hình chóp S.ABC là:
![]()
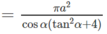

Đáp án D
Ta có:
![]()
Gọi I là trung điểm của SC. Theo định lí ba đường vuông góc ta có tam giác SAC vuông tại A, mà tam giác SBC vuông tại B nên I cách đều các đỉnh của hình chóp hay I là tâm mặt cầu ngoại tiếp hình chóp. Khi đó ta có bán kính: r = SC/2 = a

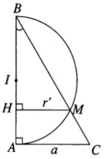
Gọi S 1 là diện tích toàn phần của hình nón và S 2 là diện tích mặt cầu.
Ta có: S 1 = πrl + πr 2 = 3 πa 2
S 2 = 4 πr 2 = 3 πa 2
Vậy S 1 = S 2
Đáp án B
Mặt cầu nội tiếp hình nón đề cho có 1 đường trong lớn nội tiếp tam giác đều (cạnh a)
Nên mặt cầu đó có bán kính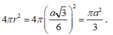
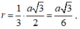
Vậy diện tích mặt cầu cần tìm là V =