Một họ nghiệm của phương trình 2sin2x - 5sinx.cosx – cos2x = -2 là ...
Đọc tiếp
Một họ nghiệm của phương trình 2sin2x - 5sinx.cosx – cos2x = -2 là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 2 2017
Phương trình ⇔ 2 sin 2 x + 3 3 sin x cos x − cos 2 x = 2 sin 2 x + cos 2 x
⇔ 3 3 sin x cos x − 3 cos 2 x = 0 ⇔ 3 cos x 3 sin x − cos x = 0.
= cos x = 0 ⇔ x = π 2 + k π k ∈ ℤ → k = 0 x = π 2 .
= 3 sin x − cos x = 0 ⇔ 3 sin x = cos x
⇔ tan x = 1 3 ⇔ tan x = tan π 6 ⇔ x = π 6 + k π k ∈ ℤ → k = 0 x = π 6 .
Vậy tập nghiệm của phương trình chứa các nghiệm π 6 và π 2 .
Chọn đáp án B.
CM
30 tháng 3 2019
Hướng dẫn giải:
Chọn A.
không là nghiệm của phương trình
Chia 2 vế phương trình cho cos2x ta được
CM
10 tháng 10 2018
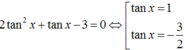
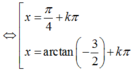
Hướng dẫn giải
Chọn C.
TH1: Nếu cosx =0 có sin2x = 1 không thỏa mãn phương trình.
TH2: 
chia cả hai vế của phương trình cho cos2x ta được:
CM
11 tháng 7 2018
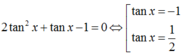
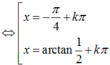
Chọn A
sin 5 x + sin 9 x + 2 sin 2 x − 1 = 0
⇔ 2 sin 7 x . c o s 2 x − c o s 2 x = 0 ⇔ c o s 2 x = 0 sin 7 x = 1 2
⇔ x = π 4 + k π 2 x = π 42 + k 2 π 7 x = 5 π 42 + k 2 π 7 , k ∈ ℤ
vậy chọn A
CM
22 tháng 7 2019
Chọn C
Ta có:
2 sin 2 x − 5 sin x . c osx -cos 2 x + 2 = 0 ⇔ 2 sin 2 x − 5 sin x . c osx -cos 2 x + 2 ( sin 2 x + c os 2 x ) = 0 ⇔ 4 sin 2 x − 5 sin x . c osx + cos 2 x = 0 ( * )
* Lại có, cos x =0 không là nghiệm của phương trình trên .
Chia cả hai vế cho cos 2 x ta được: 4 tan 2 x - 5 tan x + 1 = 0
Nên đáp án chọn là C
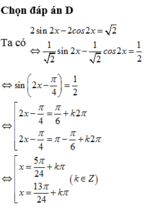
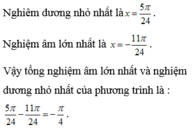
Hướng dẫn giải
Chọn C.
Chia 2 vế phương trình cho cos2x ta được