Tính thể tích khối bát diện đều cạnh a
A. a 3 2 12
B. a 3 2 6
C. a 3 2 4
D. a 3 2 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
21 tháng 8 2018
Đúng(0)
Những câu hỏi liên quan
CM
7 tháng 2 2019
Đáp án D
TXĐ: D = 0 ; 2 ta có: y ' = 2 − 2 x 2 2 x − x 2 < 0 ⇔ x > 1
Do đó hàm số nghịch biến trên 1 ; 2 .
21 tháng 8 2023
Diện tích mặt đáy là:\(\dfrac{a^2.\sqrt{3}}{4}\)
Thể tích khối lăng trụ là: \(a.\dfrac{a^2.\sqrt{3}}{4}=\dfrac{a^3.\sqrt{3}}{4}\)
\(\Rightarrow A\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 7 2021
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
Gọi M là trung điểm AB \(\Rightarrow AB\perp OM\Rightarrow AB\perp\left(SOM\right)\)
\(\Rightarrow\widehat{SMO}\) là góc giữa mặt bên và đáy hay \(\widehat{SMO}=60^0\)
\(SO=OM.tan\widehat{SMO}=\dfrac{a}{2}.tan60^0=\dfrac{a\sqrt{3}}{2}\)
\(V=\dfrac{1}{3}SO.S_{ABCD}=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{2}.a^2=\dfrac{a^3\sqrt{3}}{6}\)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
.png)
Gọi \(M\) là trung điểm của \(BC\), \(O\) là trọng tâm tam giác \(ABC\).
\( \Rightarrow SO \bot \left( {ABC} \right)\)
Tam giác \(ABC\) đều
\( \Rightarrow AM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2} \Rightarrow AO = \frac{2}{3}AM = \frac{{a\sqrt 3 }}{3}\)
Tam giác \(SAO\) vuông tại \(O \Rightarrow SO = \sqrt {S{A^2} - A{O^2}} = \frac{{a\sqrt 6 }}{3}\)
\(\begin{array}{l}{S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}\\{V_{S.ABC}} = \frac{1}{3}{S_{\Delta ABC}}.SO = \frac{{{a^3}\sqrt 2 }}{{12}}\end{array}\)
CM
1 tháng 11 2018
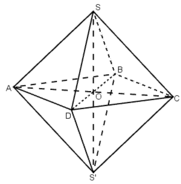
Gọi khối bát diện đều là SABCDS’ cạnh a.
* Ta chia khối bát diện thành hai khối chóp tứ giác đều bằng nhau là:
S. ABCD và S’. ABCD có cạnh bằng a.
Khi đó, 
Gọi O là giao điểm của AC và BD suy ra: SO ⊥ (ABCD)
* Ta tính thể tính khối tứ diện đều cạnh a.
Tứ giác ABCD là hình vuông cạnh a nên có diện tích là: SABCD = a 2
Ta có:
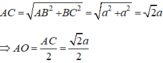
Áp dụng định lí pytago vào tam giác SOA ta có:
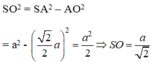
Thể tích khối tứ diện đều S.ABCD là:
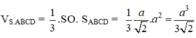
Thể tích khối bát diện đều cạnh a là:
PT
1
CM
24 tháng 9 2018
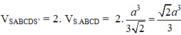
Đáp án D
Khối bát diện đều được lập từ hai khối tứ giác đều
Thể tích 1 khối chóp là V 1 = 1 3 a 2 a 2 = a 3 3 2
Thể tích khối bát diện đều là V = 2 V 1 = 2 a 3 3 2 = a 3 2 3
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
Diện tích đáy lớn là: \(S = \frac{{{{\left( {2{\rm{a}}} \right)}^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 \)
Diện tích đáy bé là: \(S' = \frac{{{a^2}\sqrt 3 }}{4}\)
Thể tích của bồn chứa là: \(V = \frac{1}{3}.\frac{{a\sqrt 6 }}{3}\left( {{a^2}\sqrt 3 + \sqrt {{a^2}\sqrt 3 .\frac{{{a^2}\sqrt 3 }}{4}} + \frac{{{a^2}\sqrt 3 }}{4}} \right) = \frac{{7\sqrt 2 }}{{12}}{a^3}\)
Chọn C.
CM
28 tháng 2 2019
Phương pháp:
Khối đa diện có các đỉnh là trung điểm của các cạnh xuất phát từ đỉnh A và F của hình bát diện đều ABCDEF (như hình vẽ) là hình hộp chữ nhật.
Cách giải:
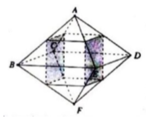
Khối đa diện có các đỉnh là trung điểm của các cạnh xuất phát từ đỉnh A và F của hình bát diện đều ABCDEF là hình hộp chữ nhật có đáy là hình vuông cạnh a 2 ;
