Giải Phương trình sau:
( x2 - 2x +4 )( x2 +3x + 4 ) = 14x2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 3 2021
1) Ta có: \(x^2-4x+4=0\)
\(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x-2=0\)
hay x=2
Vậy: S={2}
PN
11 tháng 5 2021
\(a,x^2-10x=-25\)
\(< =>x^2-10x+25=0\)
\(< =>\left(x-5\right)^2=0< =>x=5\)
b, \(4x^2-4x=-1\)
\(< =>4x^2-4x+1=0\)
\(< =>\left(2x-1\right)^2=0< =>x=\frac{1}{2}\)
HT
1
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2022
\(f\left(x\right)=\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x^2-5x+6\right)\left(5-x\right)}>0\)
\(\Leftrightarrow\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x-2\right)\left(x-3\right)\left(5-x\right)}>0\)
Bảng xét dấu:
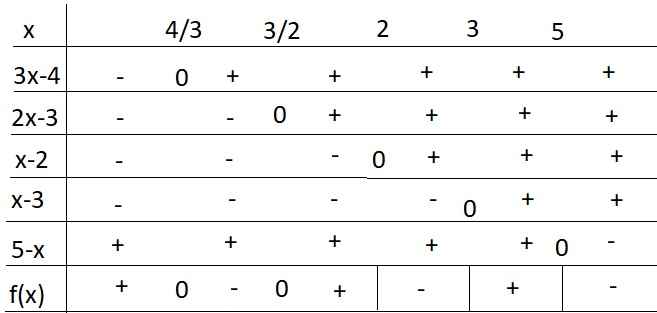
Từ bảng xét dấu ta thấy nghiệm của BPT là: \(\left[{}\begin{matrix}x< 5\\\dfrac{3}{2}< x< 2\\3< x< 5\end{matrix}\right.\)
CM
23 tháng 6 2019
Đáp số của bài toán đúng nhưng lời giải của bạn Hà chưa đầy đủ.
Lời giải của bạn Hà thiếu bước tìm điều kiện xác định và bước đối chiếu giá trị của x tìm được với điều kiện để kết luận nghiệm.
Trong bài toán trên thì điều kiện xác định của phương trình là:
x ≠ - 3/2 và x ≠ - 1/2
So sánh với điều kiện xác định thì giá trị x = - 4/7 thỏa mãn.
Vậy x = - 4/7 là nghiệm của phương trình.
CM
28 tháng 11 2017
a)
( x − 3 ) 2 + ( x + 4 ) 2 = 23 − 3 x ⇔ x 2 − 6 x + 9 + x 2 + 8 x + 16 = 23 − 3 x ⇔ x 2 − 6 x + 9 + x 2 + 8 x + 16 + 3 x − 23 = 0 ⇔ 2 x 2 + 5 x + 2 = 0
Có a = 2; b = 5; c = 2 ⇒ Δ = 5 2 – 4 . 2 . 2 = 9 > 0
⇒ Phương trình có hai nghiệm:
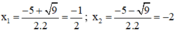
Vậy phương trình có tập nghiệm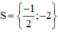 
b)
x 3 + 2 x 2 − ( x − 3 ) 2 = ( x − 1 ) x 2 − 2 ⇔ x 3 + 2 x 2 − x 2 − 6 x + 9 = x 3 − x 2 − 2 x + 2 ⇔ x 3 + 2 x 2 − x 2 + 6 x − 9 − x 3 + x 2 + 2 x − 2 = 0 ⇔ 2 x 2 + 8 x − 11 = 0
Có a = 2; b = 8; c = -11 ⇒ Δ ’ = 4 2 – 2 . ( - 11 ) = 38 > 0
⇒ Phương trình có hai nghiệm:
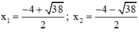
Vậy phương trình có tập nghiệm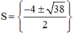 
c)
( x − 1 ) 3 + 0 , 5 x 2 = x x 2 + 1 , 5 ⇔ x 3 − 3 x 2 + 3 x − 1 + 0 , 5 x 2 = x 3 + 1 , 5 x ⇔ x 3 + 1 , 5 x − x 3 + 3 x 2 − 3 x + 1 − 0 , 5 x 2 = 0 ⇔ 2 , 5 x 2 − 1 , 5 x + 1 = 0
Có a = 2,5; b = -1,5; c = 1
⇒ Δ = ( - 1 , 5 ) 2 – 4 . 2 , 5 . 1 = - 7 , 75 < 0
Vậy phương trình vô nghiệm.
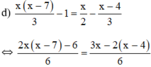
⇔ 2 x ( x − 7 ) − 6 = 3 x − 2 ( x − 4 ) ⇔ 2 x 2 − 14 x − 6 = 3 x − 2 x + 8 ⇔ 2 x 2 − 14 x − 6 − 3 x + 2 x − 8 = 0 ⇔ 2 x 2 − 15 x − 14 = 0
Có a = 2; b = -15; c = -14
⇒ Δ = ( - 15 ) 2 – 4 . 2 . ( - 14 ) = 337 > 0
⇒ Phương trình có hai nghiệm:
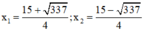
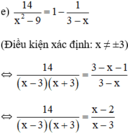
⇔ 14 = ( x - 2 ) ( x + 3 ) ⇔ 14 = x 2 - 2 x + 3 x - 6 ⇔ x 2 + x - 20 = 0
Có a = 1; b = 1; c = -20
⇒ Δ = 1 2 – 4 . 1 . ( - 20 ) = 81 > 0
Phương trình có hai nghiệm:
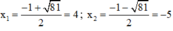
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình có tập nghiệm S = {-5; 4}.
f) Điều kiện: x≠-1;x≠4
Ta có: a= 1, b = -7, c = - 8
∆ = ( - 7 ) 2 – 4 . 1 . ( - 8 ) = 81
=> Phương trình có hai nghiệm:
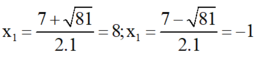
Kết hợp với diều kiện, nghiệm của phương trình đã cho là x = 8
CM
5 tháng 6 2017
Đặt m= x 2 -3x +2
Ta có: ( x 2 -3x +4)( x 2 -3x +2) =3
⇔ [( x 2 -3x +2 +2)( x 2 -3x +2) -3 =0
⇔ x 2 - 3 x + 2 2 +2( x 2 -3x +2) -3 =0
⇔ m 2 +2m -3 =0
Phương trình m 2 +2m -3 = 0 có hệ số a = 1, b = 2 , c = -3 nên có dạng
a +b+c=0
suy ra : m 1 =1 , m 2 =-3
Với m 1 =1 ta có: x 2 -3x +2 =1 ⇔ x 2 -3x +1=0
∆ = - 3 2 -4.1.1 = 9 -4 =5 > 0
∆ = 5
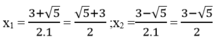
Với m 2 =-3 ta có: x 2 -3x +2 =-3 ⇔ x 2 -3x +5=0
∆ = - 3 2 -4.1.5 = 9 -20 =-11 < 0.Phương trình vô nghiệm
Vậy phương trình đã cho có 2 nghiệm :
2
28 tháng 1 2023
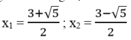
`a)(2x-1)^2-0,25=0`
`<=>(2x-1-0,5)(2x-1+0,5)=0`
`<=>(2x-1,5)(2x-0,5)=0`
`<=>[(x=0,75)(x=0,25):}`
`b)x^2+9=6x`
`<=>(x-3)^2=0`
`<=>x-3=0`
`<=>x=3`
`c)(x^2-4)-3x-6=0`
`<=>(x-2)(x+2)-3(x+2)=0`
`<=>(x+2)(x-2-3)=0`
`<=>(x+2)(x-5)=0`
`<=>[(x=-2),(x=5):}`
28 tháng 1 2023
a: =>(2x-1-0,5)(2x-1+0,5)=0
=>(2x-1,5)(2x-0,5)=0
=>x=0,25 hoặc x=0,75
b: =>x^2-6x+9=0
=>(x-3)^2=0
=>x-3=0
=>x=3
c: =>(x-2)(x+2)-3(x+2)=0
=>(x+2)(x-5)=0
=>x=5 hoặc x=-2
CM
13 tháng 3 2019
a) (x – 1)(x2 + x + 1) – 2x = x(x – 1)(x + 1)
⇔ x3 – 1 – 2x = x(x2 – 1)
⇔ x2 – 1 – 2x = x3 – x
⇔ -2x + x = 1 ⇔ - x = 1 ⇔ x = -1
Tập nghiệm của phương trình: S = { -1}
b) x2 – 3x – 4 = 0
⇔ x2 – 4x + x – 4 = 0 ⇔ x(x – 4) + (x – 4) = 0
⇔ (x – 4)(x + 1) = 0 ⇔ x – 4 = 0 hoặc x + 1 = 0
⇔ x = 4 hoặc x = -1
Tập nghiệm của phương trình: S = {4; -1}
c) ĐKXĐ : x – 1 ≠ 0 và x2 + x + 1 ≠ 0 (khi đó : x3 – 1 = (x – 1)(x2 + x + 1) ≠ 0)
⇔ x ≠ 1
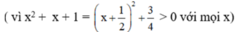
Quy đồng mẫu thức hai vế:
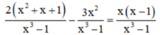
Khử mẫu, ta được: 2x2 + 2x + 2 – 3x2 = x2 – x
⇔ -2x2 + 3x + 2 = 0 ⇔ 2x2 – 3x – 2 = 0
⇔ 2x2 – 4x + x – 2 = 0 ⇔ 2x(x – 2) + (x – 2) = 0
⇔ (x – 2)(2x + 1) = 0 ⇔ x – 2 = 0 hoặc 2x + 1 = 0
⇔ x = 2 hoặc x = -1/2(thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {2 ; -1/2}
d) ĐKXĐ : x – 5 ≠ 0 và x – 1 ≠ 0 (khi đó : x2 – 6x + 5 = (x – 5)(x – 1) ≠ 0)
Quy đồng mẫu thức hai vế :
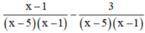
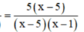
Khử mẫu, ta được : x – 1 – 3 = 5x – 25 ⇔ -4x = -21
⇔ x = 21/4 (thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {21/4}
nhan xet: x=0 ko la nghiem cua phuong trinh tren nen chia ca 2 ve cua phuong trinh cho x^2 ta duoc:
(x-2+4/x)(x+3+4/x)=14 (*)
xong rồi cậu đặt ẩn phụ là x+4/x=t thì (*) trở thành (t-2(t+3)=14 rồi giải bình thg