Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Qua M vẽ đường thẳng song song với AB cắt AC tại P và vẽ đường thẳng song song với CD cắt BD tại Q. Ta có mp (MNPQ) song song với cả AB và CD. Từ đó ( A B , C D ^ ) = ( M P , M Q ^ ) = P M Q ^
Áp dụng tính chất đường trung bình trong tam giác (do M, N là các trung điểm) ta suy ra được M P = M Q = N P = N Q = a hay tứ giác MPNQ là hình thoi.
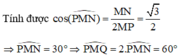
Đáp án C
Gọi P là trung điểm của AC.
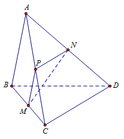
Ta có: P N / / C D , M P / / A B ⇒ A B ; C D = M P ; P N
P N = M P = a 2 , M N = a 3 2 ⇒ cos M P N ⏜ = − 1 2 ⇒ M P N ⏜ = 120 °
⇒ A B ; C D ⏜ = 60 °
Đáp án B
Gọi E là trung điểm AC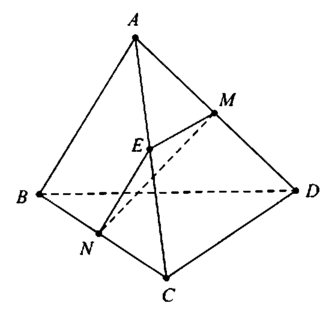
Khi đó NE//AB suy ra A B ; M N ^ = N E ; M N ^
Do đó [ E N M ^ = 30 ° E N M ^ = 150 °
Lại có N E = A B 2 = a 2 ; M E = a 2 nên tam giác MNE cân tại E suy ra E N M ^ = 30 ° ⇒ N E M ^ = 120 °
Suy ra M N = M E 2 + N E 2 - 2 M E . N E . cos N E M ^ = a 3 2 .
tham khảo:
Gọi I là trung điểm của BD.
Tam giác BCD có IM là đường trung bình nên IM//DC và IM=\(\dfrac{1}{2}\)CD=\(\dfrac{1}{2}\).2a=1
Tam giác ABD có IN là đường trung bình nên IN//AB và IN=\(\dfrac{1}{2}\)AB=\(\dfrac{1}{2}\).2a=1
Ta có: cos\(\widehat{MIN}\)=\(\dfrac{a^2+a^2-\left(a\sqrt{3}\right)^2}{2.a.a}=\dfrac{-1}{2}\)
Nên \(\widehat{MIN}\)=\(120^0\)
Do AB//IN, CD//IM nên góc giữa AB và CD là góc giữa IM và IN là bằng \(120^0\)
Đáp án C
Qua M vẽ đường thẳng song song với AB cắt AC tại P và vẽ đường thẳng song song với CD cắt BD tại Q. Ta có mp (MNPQ) song song với cả AB và CD. Từ đó
Áp dụng tính chất đường trung bình trong tam giác (do M, N là các trung điểm) ta suy ra được MP = MQ = NP = a hay tứ giác MPNQ là hình thoi.
Tính được