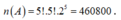Có hai dãy ghế đối diện nhau, mỗi dãy có 5 ghế. Xếp ngẫu nhiên 10 học sinh, gồm 5 nam và 5 nữ ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Tính xác suất để mỗi học sinh nam đều ngồi đối diện một học sinh nữ.
A
.
1
252
B
.
1
945
C
.
8
63
D
.
4
63
...
Đọc tiếp
Có hai dãy ghế đối diện nhau, mỗi dãy có 5 ghế. Xếp ngẫu nhiên 10 học sinh, gồm 5 nam và 5 nữ ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Tính xác suất để mỗi học sinh nam đều ngồi đối diện một học sinh nữ.
A . 1 252
B . 1 945
C . 8 63
D . 4 63
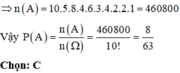
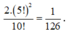
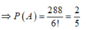
Chọn C
Số phần tử của không gian mẫu: .
Gọi biến cố : “Xếp 10 học sinh vào 10 ghế sao cho mỗi học sinh nam đều ngồi đối diện một học sinh nữ”.
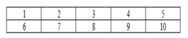
Giả sử đánh vị trí ngồi như bảng sau:
Cách 1: Xếp vị trí A 1 có 10 cách. Mỗi cách xếp vị trí A 1 sẽ có 5 cách xếp vị trí B 1 .
Mỗi cách xếp vị trí A 1 , B 1 có 8 cách xếp vị trí , tương ứng sẽ có 4 cách xếp vị trí B 2 .
Cứ làm như vậy thì số cách xếp thỏa mãn biến cố là:
Cách 2: Đánh số cặp ghế đối diện nhau là C1, C2, C3, C4, C5
Xếp bạn nam vào 5 cặp ghế có 5! cách.
Ở mỗi cặp ghế, ta có 2 cách xếp một cặp nam, nữ ngồi đối diện.
Số phần tử của A là: