Cho khối chóp tứ giác S.ABCD có đáy là hình bình hành, AD=4a, SA=SB=SC= a 6 Khi khối chóp S.ABCD có thể tích đạt giá trị lớn nhất, sin của góc giữa hai mặt phẳng (SBC) và (SCD) bằng
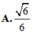
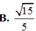
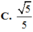
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là độ dài cạnh đáy của chóp đều S.ABCD .
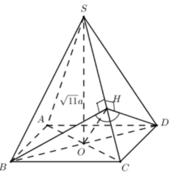
Gọi
![]()
Ta có:

Ta có:
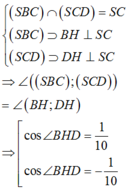
Dễ dàng chứng minh được

cân tại H.
Xét tam giác SBC ta có:

Xét tam giác BDH có:
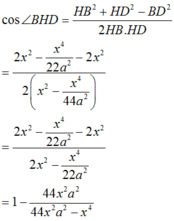
TH1:
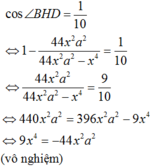
TH2:

Xét tam giác vuông SOA có:
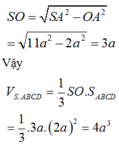
Chọn C.

Chọn D.
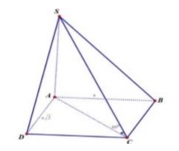
Theo giả thiết góc giữa SC và đáy bằng 60 o suy ra S C A ^ = 60 o
ABCD là hình chữ nhật nên A C = A B 2 + B C 2 = a 3
Tam giác SAC vuông tại A nên S A = A C . tan 60 o = 3 a
Diện tích đáy là S A B C D = A B . A D = 2 a 2
Thể tích khối chóp S.ABCD là V = 1 3 2 a 2 . 3 a = 2 a 3

Đáp án A
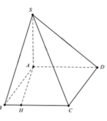
Dựng trục tọa độ với A 0 ; 0 ; 0 ; 0 ; 4 a ; 0 ; S 0 ; 0 ; 2 a 3
Ta có: A H = A B sin 60 0 = 3 a 3 2 ; B H = 3 a 2
Do đó B = 3 a 3 2 ; − 3 a 2 ; 0 ; C 3 a 3 2 ; 5 a 2 ; 0
Khi đó n S B C ¯ = k S B ¯ ; B C ¯ = 4 ; 0 ; 3 ; n S C D ¯ = k S C ¯ ; D C ¯ = 3 ; 3 ; 2 3
Do đó cos S B C ; S C D ^ = 10 3 4 2 + 3 2 24 = 1 2 ⇒ S B C ; S C D ^ = 45 0
ĐÁP ÁN: B