Trong mặt phẳng cho 10 điểm phân biệt. Số vectơ khác 0 ⇀ , có điểm đầu và điểm cuối lấy trong các điểm đã cho là
A . 2 10
B . A 10 2
C. 10!
D . C 10 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tập X = {A, B, C, D, E ; F}. Với mỗi cách chọn hai phần tử của tập X và sắp xếp theo một thứ tự ta được một vectơ thỏa mãn yêu cầu
Mỗi vectơ thỏa mãn yêu cầu tương ứng cho ta một chỉnh hợp chập 2 của 6 phần tử thuộc tập X.
Vậy số các vectơ thỏa mãn yêu cầu bằng số tất cả các chỉnh hợp chập 2 của 6, bằng
Chọn C.

Mỗi cặp sắp thứ tự gồm hai điểm (A; B) cho ta một vectơ có điểm đầu A và điểm cuối B và ngược lại.
Như vậy, mỗi vectơ có thể xem là một chỉnh hợp chập 2 của tập hợp 6 điểm đã cho.
Suy ra có A 6 2 = 30 cách.
Chọn đáp án D.

Đáp án D
Phương pháp:
Sử dụng quy tắc nhân.
Cách giải:
Số cách chọn điểm đầu là 2018 cách.
Số cách chọn điểm cuối là 2017 cách (trừ vector không).
Vậy có 2018 × 2017 = 4070306 cách

Chọn đáp án D.
Mỗi cách lấy có thứ tự hai điểm trong 2019 điểm đã cho ta xác định được một vectơ. Vì vậy, từ 2019 điểm phân biệt, ta xác định được A 2019 2 vecto khác 0 →

Chọn A
Hai điểm bất kì trong n điểm trên tạo thành hai véctơ thỏa mãn yêu cầu bài toán. Nên số các véc tơ đó là: ![]()
Nhận xét: Có thể hiểu mỗi véctơ là một chỉnh hợp chập 2 của n điểm. Nên số véctơ là:
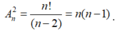

a) Có hai véc tơ.
b)
Số đoạn thẳng tạo thành từ 3 điểm A, B, C là:\(\dfrac{3.2}{2}=3\) đoạn.
Mỗi đoạn thẳng tạo thành hai véc tơ đối nhau nên số véc tơ là:
\(3.2=6\) (véc tơ).
b) Số đoạn thẳng tạo thành từ 4 điểm phân biệt là:
\(4.3:2=6\) (đoạn).
Số véc tơ tạo thành là:
6.2 = 12 (véc tơ).
Chọn B
Số vectơ khác 0 ⇀ , có điểm đầu và điểm cuối lấy từ 10 điểm phân biệt trong mặt phẳng là A 10 2