Sắp xếp 20 người vào 2 bàn tròn A, B phân biệt, mỗi bàn gồm 10 chỗ ngồi. Số cách sắp xếp là
A. C 20 10 .9!.9!
B. C 20 10 .10!.10!
C. C 20 10 . 9 ! . 9 ! 2
D. 2 C 20 10 .9!.9!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 8 2017
• Giai đoạn 1: Chọn 10 người từ 20 người xếp vào bàn A nên có C 20 10 cách chọn người. Tiếp theo là 10 người vừa chọn này có 9! cách chọn chỗ ngồi. Vậy giai đoạn 1 có C 20 10 .9! cách.
• Giai đoạn 2: 10 người còn lại xếp vào bàn B, 10 người này có 9! cách chọn chỗ ngồi. Vậy giai đoạn 2 có 9! cách.
Vậy có tất cả C 20 10 . 9 ! . 9 ! cách thỏa mãn bài toán. Chọn B.
CM
28 tháng 4 2019
Đáp án D.
Cố định em bé 
Có 2 cách sắp xếp 2 vợ chông và 7! Cách sắp xếp 7 người còn lại 
Có 2.7! cách sắp xếp.
PT
1
CM
26 tháng 2 2017
Đáp án C
Số cách sắp xếp 6 học sinh vào một bàn dài có 10 chỗ ngồi là số chỉnh hợp chập 6 của 10 phần tử. Vậy số cách sắp xếp là: A 10 6
CM
15 tháng 7 2019
a) Xếp 6 nam vào 6 ghế cạnh nhau. Có 6! cách.
Giữa các bạn nam có 5 khoảng trống cùng hai đầu dãy, nên có 7 chỗ có thể đặt ghế cho nữ.
Bây giờ chọn 4 trong 7 vị trí để đặt ghế. Có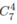 
cách.
Xếp nữ vào 4 ghế đó. Có 4! cách.
Vậy có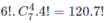 
cách xếp mà không có hai bạn nữ nào ngồi cạnh nhau.
b) Xếp 6 ghế quanh bàn tròn rồi xếp nam vào ngồi. Có 5! cách.
Giữa hai nam có khoảng trống. Xếp 4 nữ vào 4 trong 6 khoảng trống đó. Có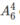 
cách.
Theo quy tắc nhân, có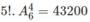 
cách.
5 tháng 10 2021
a) Có 2 cách xếp.
Bạn A có 6! cách.
Bạn B có 6! cách.
Đổi vị trí A,B có tất cả 2*(6!)2 cách xếp chỗ.
b) Chọn 1 học sinh A vào vị trí bất kì: 12 cách.
Chọn 1 học sinh B đối diện A có 6 cách.
Cứ chọn liên tục như vậy ta được:
\(\left(12\cdot6\right)\cdot\left(10\cdot5\right)\cdot\left(8\cdot4\right)\cdot\left(6\cdot3\right)\cdot\left(4\cdot2\right)\cdot\left(2\cdot1\right)=2^6\cdot\left(6!\right)^2\)
cách xếp chỗ để hai bạn ngồi đối diện thì kkhasc trường nhau.
DD
Đoàn Đức Hà
Giáo viên
25 tháng 12 2022
- Đếm số cách để A và B ngồi cạnh nhau, C ngồi vị trí bất kì:
Coi A, B là một người, có \(2!\) cách xếp vị trí A, B.
Khi đó ta xếp vị trí của 9 người: \(9!\).
Có tổng số cách xếp là: \(2!.9!\).
- Đếm số cách để A và B ngồi cạnh nhau, C ngồi cạnh A.
Coi A, B, C là một người. Có 2 cách xếp thỏa mãn là CAB, BAC.
Khi đó ta xếp vị trí của \(8\) người: \(8!\).
Có số cách xếp là: \(2.8!\).
Vậy số cách xếp để A và B ngồi cạnh nhau, A và C không ngồi cạnh nhau là \(2!.9!-2.8!\).
Chọn A
Giả sử khi xếp 10 người vào một bàn tròn, hai cách sắp xếp được xem là như nhau nếu cách này nhận được từ cách kia bằng cách xoay bàn đi một góc nào đó.
Bài toán trên được chia thành các công đoạn sau:
Công đoạn 1: Chọn 10 người trong 20 người đã cho để xếp vào bàn tròn A: có C 20 10 cách.
Công đoạn 2: Sắp xếp 10 người vừa chọn được ở công đoạn 1 vào bàn tròn A: có 9! cách.
Công đoạn 3: Sắp xếp 10 người còn lại vào bàn tròn B: có 9! cách.
Vậy số cách sắp xếp là: C 20 10 .9!.9! cách.