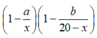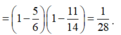Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C.
Phương pháp:
Tính xác suất theo định nghĩa P A = n A n Ω với n(A) là số phần tử của biến cố A , n ( Ω ) la số phân tử của không gian mẫu.
+ Chú ý rằng: Nếu số được lấy ra có chữ số đứng trước nhỏ hơn chữ số đứng sau thì không thể có số 0 trong số đó.
Cách giải: + Số có 6 chữ số khác nhau là a b c d e f với a , b , c , d , e , f ∈ 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9
Nên a có 9 cách chọn, b có 9 cách chọn, c có 8 cách chọn, d có 7 cách chọn, e có 6 cách chọn và f có 5 cách chọn.Suy ra số phần tử của không gian mẫu n Ω = 9 . 9 . 8 . 7 . 6 . 5 = 136080
+ Gọi A là biến cố a b c d e f là số lẻ và a < b < c < d < e < f
Suy ra không thể có chữ số 0 trong số a b c d e f và f ∈ 7 ; 9 .
+ Nếu f = 7 ⇒ a , b , c , d , e ∈ 1 ; 2 ; 3 ; 4 ; 5 ; 6 mà với mỗi bộ 5 số được lấy ra ta chỉ ó duy nhất 1 cách sắp xếp theo thứ tự tăng dần nên có thể lập được C 6 5 = 6 số thỏa mãn.
+ Nếu f = 9 ⇒ a , b , c , d , e ∈ 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 mà với mỗi bộ 5 số được lấy ra ta chỉ ó duy nhất 1 cách sắp xếp theo thứ tự tăng dần nên có thể lập được C 8 5 = 56 số thỏa mãn.
Suy ra n A = 6 + 56 = 62 nên xác suất cần tìm là P A = n A n Ω = 62 136080 = 31 68040
Èo toàn bài khó nhằn :( Thôi làm được mỗi câu 2, câu 1 thì...dẹp đi
\(n\left(\Omega\right)=9.9.8.7.6.5\)
Số lẻ vậy thì f={1;3;5;7;9}
Nhưng nếu f=1 thì ko tồn tại a thỏa mãn a<f do a khác 0
f=3 cũng ko thỏa mãn do nếu a=1; b=2; nhưng ko tồn tại c thỏa mãn :v
f=5 tương tự, ko tồn tại e thỏa mãn
=> f={7;9}
Nếu f=7 thì (a,b,c,d,e)={1;2;3;4;5;6} và chỉ có duy nhất 1 cách sắp xếp \(\Rightarrow C^5_6\left(cach\right)\)
Nếu f=9 thì (a,b,c,d,e)={1;2;3;4;5;6;7;8} và chỉ có duy nhất một cách xếp \(\Rightarrow C^5_8\left(cach\right)\)
\(\Rightarrow n\left(A\right)=C^5_6+C^5_8\) \(\Rightarrow p\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=...\)
Gọi A là số tự nhiên có 8 chữ số a1a2a3a4a5a6a7a8 chia hết cho 1111
9999a1a2a3a4 + a1a2a3a4+a5a6a7a8 để A chia hết cho 1111 thì a1a2a3a4+a5a6a7a8 chia hết cho 1111
1000(a1 + a5) + 100(a2 + a6) + 10(a3 + a7) + (a4+ a8) (1) chia hết cho 1111
đặt (a1 + a5) = x
(a2 + a6) = y
(a3 + a7) = z
(a4+ a8) = t
3<=x<=15
xét đk
suy ra x = 9
suy ra x=y=z=t= 9
suy ra x+y+z+t=36 suy ra t= 36-x-y-z
thế vào (1) suy ra
999(a1 + a5) + 99(a2 + a6) + 9(a3 + a7) =36
hoán vị .......
suy ra có 3840 số
Chọn D
Gọi số có 6 chữ số có dạng 
Từ 10 chữ số {0;1;2;3;4;5;6;7;8;9}, ta lập được 9. A 9 5 số có 6 chữ số đôi một khác nhau.
Lấy ngẫu nhiên một số từ tập X 
Gọi A là biến cố “Lấy một số thuộc X luôn chứa đúng ba số thuộc tập Y = {1;2;3;4;5} và 3 số đứng cạnh nhau, số chẵn đứng giữa hai số lẻ ”.
Ta coi 3 vị trí liền nhau trong X là một phần tử Z, sắp xếp 3 chữ số khác nhau trong Z thỏa mãn biến cố :
+ Số thứ nhất là số lẻ thuộc Y có 3 cách chọn.
+ Số thứ hai là số chẵn thuộc Y có 2 cách chọn.
+ Số thứ ba là số lẻ thuộc Y có 2 cách chọn.
Áp dụng quy tắc nhân ta có 12 cách sắp xếp phần tử .
Trường hợp 1: Số có 6 chữ số có dạng 
+) z có 12 cách chọn.
+) Xếp 5 chữ số còn lại khác các số tập Y vào 3 vị trí 
Áp dụng quy tắc nhân, ta lập được 
Trường hợp2: Số có 6 chữ số có dạng 
+)
a
1
có 4 cách chọn 
+) Xếp z vào 3 vị trí, z có 12 cách chọn nên có 36 cách sắp xếp.
+) Xếp 4chữ số còn lại vào 2 vị trí 
Áp dụng quy tắc nhân, ta lập được 4.36. A 4 2 = 1728 số có 6 chữ số đôi một khác nhau thỏa mãn.
Vậy ta có tất cả 
(số) thoả mãn yêu cầu bài toán.
Chọn B
Số phần tử của tập hợp E là 
Vì 
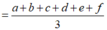
Mà chia hết cho 3 nên khi lấy ra 6 chữ số thỏa điều kiện ta phải loại ra một số chia hết cho 3. Ta có 3 trường hợp sau:
1) Trường hợp 1:
Loại bỏ số 0, khi đó a + b = c + d = e + f = 7
Bước 1: Chia ra làm 3 cặp số có tổng bằng 7 là : (1;6), (2;5), (3;4) có 1 cách chia.
Bước 2: Chọn a có 6 cách; chọn b có 1 cách; chọn c có 4 cách; chọn d có 1 cách; chọn e có 2 cách; chọn f có 1 cách: có 6.1.4.1.2.1 = 48 cách.
Trường hợp này có 48 số.
2) Trường hợp 2:
Loại bỏ số 3, khi đó a + b = c + d = e + f = 6
Bước 1: Chia ra làm 3 cặp số có tổng bằng 6 là : (0;6), (1;5), (2;4) có 1 cách chia.
Bước 2: Chọn a có 5 cách (vì có số 0); chọn b có 1 cách; chọn c có 4 cách; chọn d có 1 cách; chọn e có 2 cách; chọn f có 1 cách: có 5.1.4.1.2.1 = 40 cách.
Trường hợp này có 40 số.
3) Trường hợp 3:
Loại bỏ số 6, khi đó a + b = c + d = e + f = 5. Tương tự như trường hợp 2, có 40 số.
Vậy trong tập hợp E có tất cả 48 + 40 + 40 = 128 số có dạng a b c d e f ¯ sao cho a + b = c + d = e + f
Xác suất cần tìm là: 
"Một số lẻ chữ số 1 và 1 số chẵn chữ số 2" nghĩa là sao nhỉ?
Bạn có thể ghi 1 cách chính xác tuyệt đối đề bài không?
Chọn C
Gọi x là số bi của hộp thứ nhất nên số bi ở hộp thứ hai là 20 - x 
)
Gọi a,b 
lần lượt là số bi xanh hộp thứ nhất và số bi xanh ở hộp thứ hai.
Suy ra: 0 < a < x, 0 < b < 20 - x
Số cách lấy bi ở mỗi hộp là độc lập với nhau nên ta đặt:
+) Xác suất lấy một bi xanh ở hộp thứ nhất là a x và ở hộp thứ hai là b 20 - x
Với a, b, x là các số tự nhiên thỏa mãn 
+) Xác suất lấy được hai bi xanh 
Ta có 
Lập bảng thử từng giá trị
Khi đó, các giá trị của x là 6 hoặc 84
Ta lại có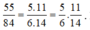 
Do đó, 
hoặc ngược lại
Vậy xác suất để lấy được hai viên bi đỏ là
