Cho tứ diện đều ABCD cạnh bằng a. Gọi M là trung điểm của CD. Tính khoảng cách giữa hai đường thẳng AC và BM ...
Đọc tiếp
Cho tứ diện đều ABCD cạnh bằng a. Gọi M là trung điểm của CD. Tính khoảng cách giữa hai đường thẳng AC và BM
K
Khách
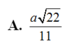
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 3 2016
Đặt \(\overrightarrow{DA}=\)\(\overrightarrow{a}\) , \(\overrightarrow{DB}=\overrightarrow{b},\overrightarrow{DC}=\overrightarrow{c}\) với \(\left|\overrightarrow{a}\right|=\left|\overrightarrow{b}\right|=\left|\overrightarrow{c}\right|=a\) và \(\overrightarrow{a}.\overrightarrow{b}=\overrightarrow{b}.\overrightarrow{c}=\overrightarrow{c}.\overrightarrow{a}=\frac{a^2}{2}\) như hình vẽ
Do M là trung điểm AB nên \(\overrightarrow{DM}=\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}\)
do đó \(\overrightarrow{CM}=\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}-\overrightarrow{c}\)
Xét điểm \(N\in AC\), giả sử \(\overrightarrow{NA}=t.\overrightarrow{NC}\), \(t\ne1\). Khi đó \(\overrightarrow{DN}=\frac{\overrightarrow{a}-t\overrightarrow{c}}{1-t}\)
Vậy \(DN\perp CM\Rightarrow\overrightarrow{DN}.\overrightarrow{CM}=0\Leftrightarrow\left(\overrightarrow{a}+\overrightarrow{b}-2\overrightarrow{c}\right)\left(\overrightarrow{a}-t\overrightarrow{c}\right)=0\Leftrightarrow t=\frac{1}{2}\)
Từ đó , với \(N\in AC\) mà \(\overrightarrow{NC}=-2\overrightarrow{NA}\) thì \(DN\perp CM\) và khi đó
\(\overrightarrow{DN}=\frac{2}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{c}\)
Giả sử UV là đoạn vuông góc chung của CM, DN với \(U\in CM,V\in DN\) và \(\overrightarrow{CU}=u\overrightarrow{CM}=\frac{u}{2}.\overrightarrow{a}+\frac{u}{2}.\overrightarrow{b}-u.\overrightarrow{c},\overrightarrow{DV}=v.\overrightarrow{DN}=\frac{2v}{3}.\overrightarrow{a}+\frac{v}{3}.\overrightarrow{c}\)
Từ đó suy ra
\(\overrightarrow{UV}=\overrightarrow{DV}-\left(\overrightarrow{DC}+\overrightarrow{CU}\right)\)
\(=\left(\frac{2v}{3}-\frac{u}{2}\right)\overrightarrow{a}-\frac{u}{2}\overrightarrow{b}+\left(\frac{v}{3}+u-1\right)\overrightarrow{c}\)
Điều kiện \(\overrightarrow{UV}.\overrightarrow{CM}=0\) tương đương với :
\(\frac{1}{2}\left(\frac{2v}{3}-\frac{u}{2}\right)-\frac{u}{4}-\left(\frac{v}{3}+u-1\right)+\frac{1}{4}\left(\frac{2v}{3}-\frac{u}{2}\right)-\frac{1}{2}\left(\frac{2v}{3}-\frac{u}{2}\right)+\frac{u}{4}+\frac{1}{4}\left(\frac{v}{3}+u-1\right)+\frac{1}{4}\left(\frac{v}{3}+u-1\right)=0\)
Từ đó ta thu được \(u=\frac{2}{3}\)
Điều kiện \(\overrightarrow{UV}.\overrightarrow{DN}=0\) tương đương với :
\(\frac{2}{3}\left(\frac{2v}{3}-\frac{u}{2}\right)-\frac{u}{6}+\frac{1}{3}\left(\frac{v}{3}+u-1\right)+\frac{1}{6}\left(\frac{2v}{3}-\frac{u}{2}\right)-\frac{u}{12}+\frac{1}{3}\left(\frac{v}{3}+u-1\right)=0\)
Từ đó ta thu được \(v=\frac{6}{7}\)
Khi đó, \(\overrightarrow{UV}=\frac{5}{21}\overrightarrow{a}-\frac{7}{21}\overrightarrow{b}-\frac{1}{21}\overrightarrow{c}=\frac{1}{21}\left(5\overrightarrow{a}-7\overrightarrow{b}-\overrightarrow{c}\right)\)
Suy ra \(d\left(CM,DN\right)=UV=\sqrt{\left|\overrightarrow{UV}\right|^2}=\frac{a\sqrt{42}}{21}\)
21 tháng 8 2023
THAM KHẢO:
Tam giác ACD đều cạnh a có AK là trung tuyến nên AK=\(\dfrac{\sqrt{3}}{2}\)a
Gọi I là trung điểm của BD
Tam giác ABD đều cạnh a có AI là trung tuyến nên AI=\(\dfrac{\sqrt{3}}{2}\)a
Tam giác BCD có IK là đường trung bình nên IK//BC, IK=\(\dfrac{1}{2}\)BC=\(\dfrac{1}{2}\)a
Ta có: cos\(\widehat{AKI}\)=\(\dfrac{\left(\dfrac{\sqrt{3}}{2}\right)^2+\left(\dfrac{1}{2}\right)^2-\left(\dfrac{\sqrt{3}}{2}\right)^2}{2.\dfrac{\sqrt{3}}{2}.\dfrac{1}{2}}=\dfrac{\sqrt{3}}{6}\)
Nên \(\widehat{AKI}\)=\(73,2^0\)
Vì BC//IK nên góc giữa AK và BC là góc giữa AK và KI và bằng \(73,2^0\)
Đáp án A.