Cho hình lăng trụ tam giác đều ABC.A'B'C' có AB= 2 3 và AA'=2. Gọi M, N, P lần lượt là trung điểm của các cạnh A’B’, A’C’ và BC. Cosin của góc tạo bởi hai mặt phẳng (AB'C') và (MNP) bằng
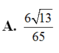
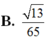
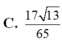
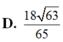
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.

Dễ thấy:
A B ' C ' ; M N P ^ = A B ' C ' ; M N C B ^
= 180 0 − A B ' C ' ; A ' B ' C ' ^ − M N B C ; A ' B ' C ' ^ = 180 0 − A ' B C ; A B C ^ − M N B C ; A B C . ^
Ta có:
M N B C ; A B C ^ = A ' P ; A P ^ = A ' P A ^ = arctan 2 3 .
Và
M N B C ; A B C ^ = S P ; A P ^ = S P A ^ = arctan 4 3 ,
với S là điểm đối xứng với A qua A’,
thì S A = 2 A A ' = 4.
Suy ra
cos A B ' C ' ; M N P ^ = c os 180 0 -arctan 2 3 − arctan 4 3 = 13 65 .

Đáp án B
Gọi L là điểm thỏa mãn A P ¯ = 3 P L ¯ và Q là trung điểm B ' C ' thì cosin cần tìm là
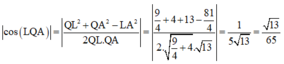

Dùng phương pháp tọa độ hóa.
Đặt hệ trục tọa độ, ở đây như thầy đã trình bày ta nên chọn gốc tại P trục Ox, Oy là PA và PC.
Gọi α góc tạo bởi hai mặt phẳng ( AB'C' ) và (MNP)
Khi đó cos α = n 1 → . n 2 → n 1 → . n 2 → = 13 65
Đáp án cần chọn là B
Đáp án B