Một hình trụ tròn xoay bán kính R=1. Trên hai đường tròn đáy (O) và (O’). Lấy A và B sao cho AB=2. Góc giữa AB và trục OO’ bằng
30
°
. Xét hai khẳng định sau: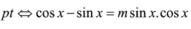
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

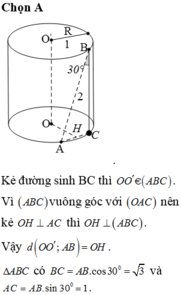
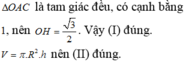

Đáp án D.
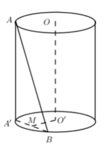
Phương pháp :
+) Xác định mặt phẳng (P) chứa AB và song song với OO’.
+) d(OO’;AB) = D(OO’;(P))
Cách giải :
Dựng AA’//OO’ ta có: (OO’;AB) = (AA’;AB) = A’AB = 300
Gọi M là trung điểm của A’B ta có:
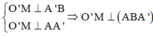
![]()
![]()
=>d(OO’;AB) = d(OO’;(ABA’)) = d(O’;(ABA’)) = O’M
Xét tam giác vuông ABA’ có ![]()
Xét tam giác vuông O’MB có 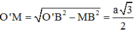

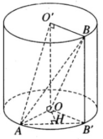
Ta có ( α ) là (ABB’). Vì OO’ // ( α ) nên khoảng cách giữa OO’ và ( α ) bằng khoảng cách từ O đến ( α ). Dựng OH ⊥ AB′ ta có OH ⊥ ( α ).
Vậy khoảng cách cần tìm là 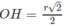

Đáp án C.
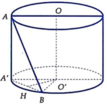
Gọi tâm hai đáy là O và O'. A ∈ O . Dựng hình chữ nhật A O O ' A ' .
Ta có A ' A B ^ = 30 ° ⇒ A ' B = A ' A . tan 30 ° = r . Suy ra tam giác A ' O ' B là tam giác đều.
Vì O O ' / / A A ' nên O O ' / / A A ' B .
Do đó d O O ' ; A B = d O O ' ; A A ' B = d O ' ; A A ' B
Gọi H là trung điểm của A'B.
⇒ O ' H ⊥ A A ' B ⇒ d O ' ; A A ' B = O H = O ' A ' 3 2 = r 3 2

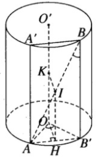
Góc giữa hai bán kính đáy OA và O’B là ∠ AOB′ và ∠ A′O′B
Vì AB’ = r nên AOB’ là tam giác đều , do đó ∠ AOB′=60 °