Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
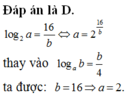
1. Ta có : \(\left(\frac{1}{a}-\frac{1}{b}\right)^2\ge0\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}\ge\frac{2}{ab}\)
Tương tự : \(\frac{1}{b^2}+\frac{1}{c^2}\ge\frac{2}{bc}\); \(\frac{1}{a^2}+\frac{1}{c^2}\ge\frac{2}{ac}\)
\(\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\ge\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}\). Dấu " = " xảy ra \(\Leftrightarrow\)a = b = c
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=3\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+2\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}\right)=9\)
\(9\le3\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)\)\(\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\ge3\)
Dấu " = " xảy ra \(\Leftrightarrow\)a = b = c = 1
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=7\)\(\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+2\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}\right)=49\)
\(\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+2.\frac{a+b+c}{abc}=49\)
\(\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}=49\)
\(\left(a+1\right)\left(b+1\right)\ge1\)
\(=>ab+a+b+1\ge1\)
\(=>1+a+b+1\ge1\)( luôn đúng ) (* )
KL : (* ) (đúng ) => \(\left(a+1\right)\left(b+1\right)\ge1\)(đúng )
KL
tuổi con HN là :
50 : ( 1 + 4 ) = 10 ( tuổi )
tuổi bố HN là :
50 - 10 = 40 ( tuổi )
hiệu của hai bố con ko thay đổi nên hiệu vẫn là 30 tuổi
ta có sơ đồ : bố : |----|----|----|
con : |----| hiệu 30 tuổi
tuổi con khi đó là :
30 : ( 3 - 1 ) = 15 ( tuổi )
số năm mà bố gấp 3 tuổi con là :
15 - 10 = 5 ( năm )
ĐS : 5 năm
mình nha
Ta có:
\(a^4+b^4\ge a^3+b^3\) \(\left(1\right)\)
\(\Leftrightarrow\) \(2\left(a^4+b^4\right)\ge\left(a+b\right)\left(a^3+b^3\right)\) (vì \(a+b=2\))
\(\Leftrightarrow\) \(a^4+b^4\ge a^3b+ab^3\)
\(\Leftrightarrow\) \(a^4-a^3b-ab^3+b^4\ge0\)
\(\Leftrightarrow\) \(a^3\left(a-b\right)-b^3\left(a-b\right)\ge0\)
\(\Leftrightarrow\) \(\left(a-b\right)\left(a^3-b^3\right)\ge0\)
\(\Leftrightarrow\) \(\left(a-b\right)^2\left(a^2+ab+b^2\right)\ge0\) \(\left(2\right)\)
Bất đẳng thức \(\left(2\right)\) luôn đúng (do \(\left(a-b\right)^2\ge0\) và \(a^2+ab+b^2=\left(a+\frac{b}{2}\right)^2+\frac{3b^2}{4}\ge0\) ), mà các phép biến đổi trên tương đương nên bất đẳng thức \(\left(1\right)\) được chứng minh.
Đẳng thức trên xảy ra khi và chỉ khi \(a=b\)
\(a^3-a^2b+ab^2-6b^3=0\)
\(\Leftrightarrow\left(a-2b\right)\left(a^2+ab+3b^2\right)=0\left(1\right)\)
Vì a>b>0 =>a2+ab+3b2>0 nên từ (1) ta có a=2b
Vậy biểu thức \(A=\frac{a^4-4b^4}{b^4-4a^4}=\frac{16b^4-4b^4}{b^4-64b^4}=\frac{12b^4}{-63b^4}=-\frac{4}{21}\)
