Cho A, B, C là ba điểm trong mặt phẳng phức theo thứ tự biểu diễn các số: - 1 + i ; - 1 - i ; 2 i . Tính A B → . A C →
A. – 7.
B. 5.
C. – 2.
D. – 6.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
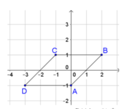
Ta có điểm A(0;-1), B(2;1), C(-1;1). Gọi D(a;b), khi đó ABCD là hình bình hành
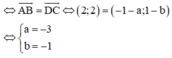
Suy ra số phức z biểu diễn D là z = -3 - i

Đáp án C.
Với bài toán này ta sẽ chọn trường hợp cụ thể thỏa mãn hai điều kiện trên, từ đó xét tam giác ABC là tam giác gì.
Chọn z 1 = 1 + 3 i ; z 2 = 1 − 3 i ; z 3 = − 2
⇒ A 1 ; 3 , B 1 ; − 3 , C − 2 ; 0 ⇒ A B = B C = C A = 2 3
Vậy ABC là tam giác đều.

Đáp án A.
Chọn z 1 = 1 ⇒ z 2 = 1 ± i 3 2 ⇒ z 2 − z 1 = − 1 ± i 3 2 .

Đáp án A.
Cách 1: Ta có:
![]()
![]()
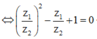
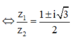
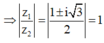
![]()
mặt khác 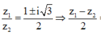
![]()
Do đó tam giác OAB là tam giác đều.
Cách 2: Chọn 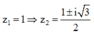
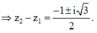
Chọn D.
Ta có, A(-1; 1); B(-1; -1); C(0; 2).