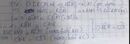Bài 1.
Cho tam giác ABC đều nội tiếp đường tròn tâm O, gọi H là trung điểm BC. Trên các cạnh AB,AC lần lượt lấy hai điểm D,Esao cho góc DHE=60 độ. Lấy M bất kì trên cung nhỏ AB.
a) Chứng minh ba đường phân giác của ba góc BAC,BDE,DEC đồng quy.
b) Cho AB có độ dài 1 đơn vị. Chứng minh: MA+MB<4/3
Bài 2.
Cho tam giác ABC không cân, vẽ phân giác trong Ax của góc A. Vẽ đường thẳng d là trung trực của đoạn thẳng BC. Gọi E là giao của Ax và d. Chứng minh E nằm ngoài tam giác ABC.
Bài 3.
Cho x,y,z là ba số thực dương thỏa điều kiện xyz=1. Chứng minh rằng:
\(\frac{1}{{1 + {x^3} + {y^3}}} + \frac{1}{{1 + {y^3} + {z^3}}} + \frac{1}{{1 + {z^3} + {x^3}}} \le 1\)