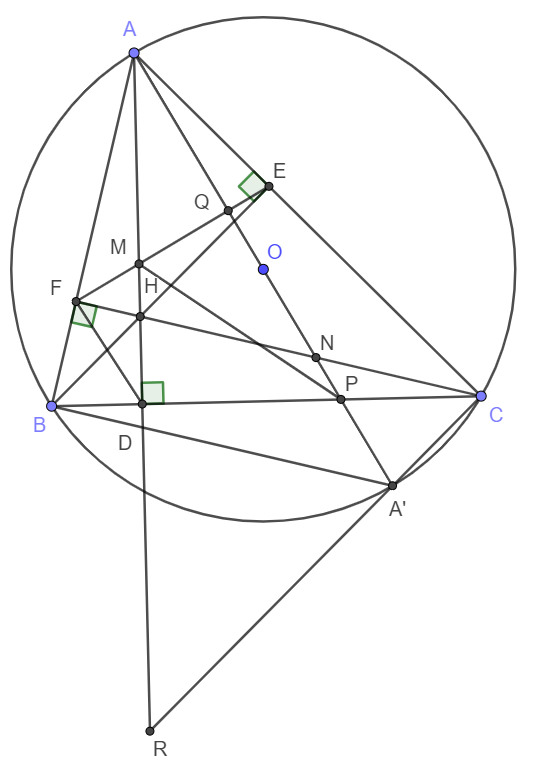
14: Cho tam giác ABC nhọn nôi tiếp (O), các đường cao AD,BE,CF đồng
qui tại H. gọi M là trung điểm của BC, P là
giao của EF với BC. Gọi K là giao của AP
với (O).
1) Chứng minh tứ giác AKHE nội tiếp
2) Chứng minh tứ giác AMDK nội tiếp
3) Chứng minh M,H,K thẳng hàng.
4) Chứng minh PH vuông góc với AM.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/ Ta có:
• Góc AHB bằng 90 độ (vì AD là đường cao của tam giác ABD).
• Góc AEB bằng góc AFB bằng 90 độ (vì AB là đường cao của tam giác AFB và AC là đường cao của tam giác AEC).
Góc AHE bằng góc AFE (vì đường cao AH đồng quy với đường chéo EF của tứ giác AHEF).
• Góc AHP bằng góc AKP bằng 90 độ (vì KA là đường đường kính của đường tròn (O)).
• Góc AEP bằng góc AFP (vì đường cao AE đồng quy với đường chéo AF của tứ giác AEPF).
Do đó, ta có thể kết luận rằng 5 điểm P, A, E, H, F nằm trên cùng một đường tròn. Để xác định tâm T của đường tròn này, ta lấy hai đường kính của đường tròn là AP và EF, sau đó kẻ đường thẳng qua giữa chúng. Đường thẳng này cắt đường tròn tại T, là tâm của đường tròn.
2/ Ta có:
• Góc AHE bằng góc AFE (vì đường cao AH đồng quy với đường chéo EF của tứ giác AHEF).
• Góc EHF bằng 90 độ (vì EF là đường cao của tam giác EHF).
o Góc FHE bằng góc FEM (vì đường cao FH đồng quy với đường chéo EM của tứ giác FHEM).
Do đó, ta có thể kết luận rằng EM và FM là hai tiếp tuyến của đường tròn (T).
3/ Ta cần chứng minh rằng tam giác DEF nội tiếp đường tròn (M). Ta có:
• Góc EHF bằng 90 độ (vì EF là đường cao của tam giác EHF).
• Góc FEM bằng góc FHE (vì đường cao FH đồng quy với đường chéo EM của tứ giác FHEM). • Góc FHE bằng góc DAE

1: Xét tứ giác BEDC có \(\widehat{BEC}=\widehat{BDC}=90^0\)
nên BEDC là tứ giác nội tiếp
2: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc BAD chung
Do đó:ΔADB\(\sim\)ΔAEC
Suy ra: AD/AE=AB/AC
hay AD/AB=AE/AC
Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
Do đó: ΔADE\(\sim\)ΔABC
hay \(\widehat{ADE}=\widehat{ABC}\)

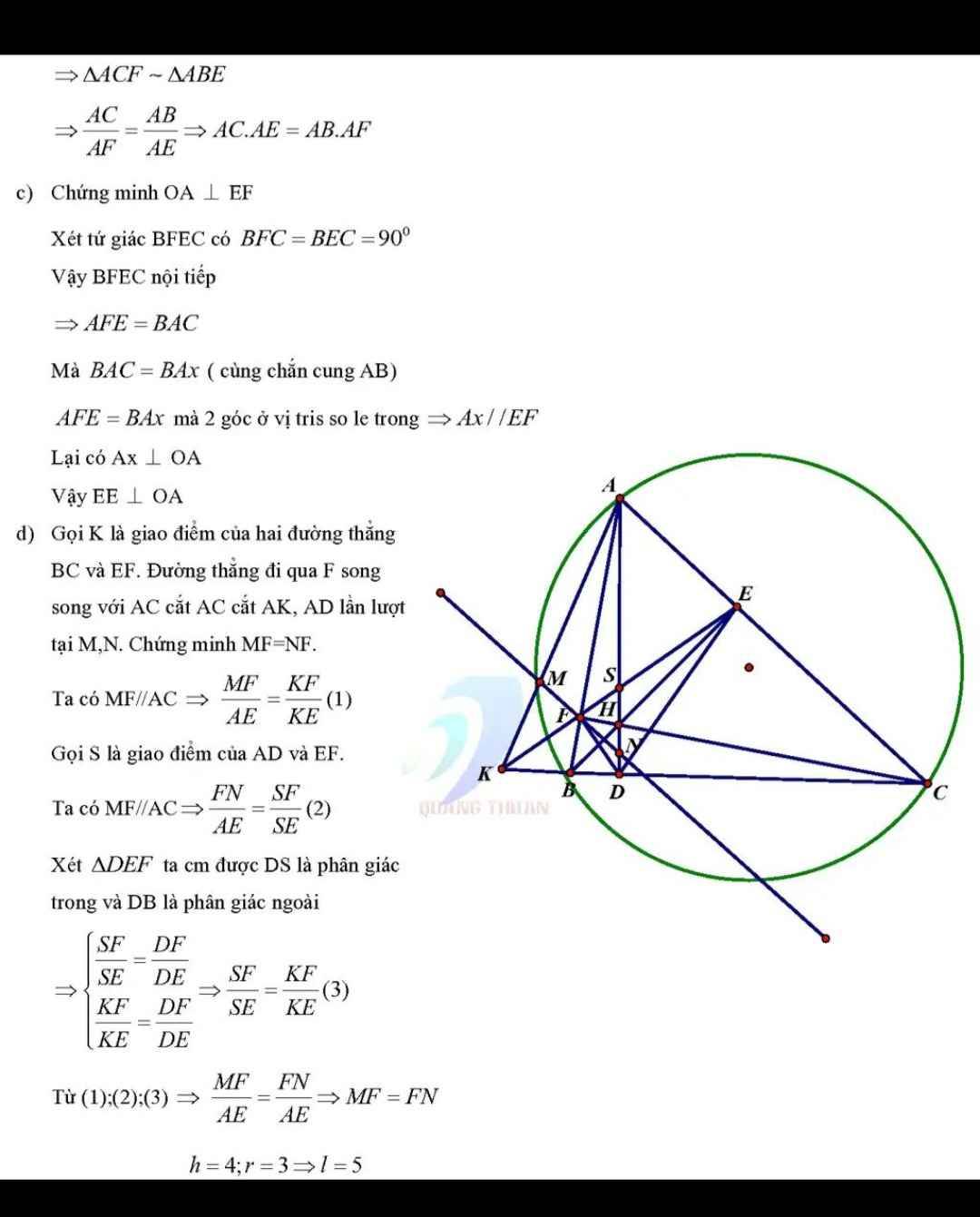
a) theo gt, BFC=BEC=90
=> BFEC nội tiếp (có 2 góc kề bang nhau)
góc AFC=ADC=90 => AFDC nội tiếp ( có 2 cạnh kề cùng nhìn một đoan thẳng bằng nhau)
b) vì tứ giác ABA'C nội tiếp => ABC = AA'C (cùng chắn cung AC)
Lại có ABC= AHF (Cùng phụ với góc BAD)
Ta thấy AFHE nội tiếp vì AFH +AEH = 90+90=180
=> AHF=AEF (Cùng chắn cung AF)
=>Đpcm
c) vì tứ giác EQA'C nôi tiếp
nên EQA'+ECA'=180 mà ECA'=90 vì là góc nội tiếp chắn nửa đường tròn
=> MQP=EQA'=90 ( vì MQP+EQA=180)
Trong đó ADC=90 =>Đpcm
d) Vì ABA'C VÀ FBDH nội tiếp nên góc NA'C=ABC=DHC
=>NA'C=DHC=>Đpcm

1: Xét tứ giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC là tứ giác nội tiếp
2: ΔADB vuông tại D có DG vuông góc AB
nên AG*AB=AD^2
ΔADC vuông tại D
mà DH là đường cao
nên AH*AC=AD^2=AG*AB
=>AH/AB=AG/AC
=>ΔAHG đồng dạng với ΔABC
=>góc AGH=góc ACB=goc AFE
=>HG//FE

1: góc ABP=1/2*sđ cung AP=90 độ
=>BP//CH
góc ACP=1/2*sđ cung AP=90 độ
=>CP//BH
mà BP//CH
nên BHCP là hình bình hành
=>BC cắt HP tại trung điểm của mỗi đường
=>M là trung điểm của HP

Gọi G là giao điểm của FC và AK.
Áp dụng định lý Menelaus cho tam giác FBC với cát tuyến A, G, K ta có:
\(\dfrac{AF}{AB}.\dfrac{KB}{KC}.\dfrac{GC}{GF}=1\Rightarrow\dfrac{GC}{GF}=\dfrac{KC}{KB}.\dfrac{AB}{AF}\). (1)
Áp dụng định lý Menelaus cho tam giác ACB với cát tuyến K, E, F ta có:
\(\dfrac{EA}{EC}.\dfrac{KC}{KB}.\dfrac{FB}{FA}=1\Rightarrow\dfrac{KC}{KB}=\dfrac{FA}{FB}.\dfrac{EC}{EA}\). (2)
Từ (1), (2) có \(\dfrac{GC}{GF}=\dfrac{EC}{EA}.\dfrac{AB}{FB}\). (*)
Mặt khác áp dụng định lý Menelaus cho tam giác AFC với cát tuyến B, H, E ta có:
\(\dfrac{HC}{HF}.\dfrac{BF}{BA}.\dfrac{EA}{EC}=1\Rightarrow\dfrac{HC}{HF}=\dfrac{AB}{FB}.\dfrac{EC}{EA}\). (**)
Từ (*), (**) ta có \(\dfrac{GC}{GF}=\dfrac{HC}{HF}\Rightarrow\dfrac{AC}{MF}=\dfrac{AC}{NF}\Rightarrow FM=FN\).