Thấu kính hội tụ có tiêu cự 5cm. A là điểm vật thật trên trục chính cách thấu kính 10cm, A' là ảnh của A. Người ta đã chứng minh được rằng AA’ là khoảng cách ngắn nhất và bằng
A. 20cm
B. 40cm
C. 10cm
D. 15cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

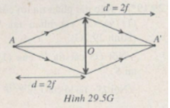
d = 2f → d’ = 2f
AA’ = d + d’ = 4f = 40cm
(Hình 29.5G)
Tổng quát với vật thật và ảnh thật:
![]()
AA’ ≥ 4f hay AA’min = 4f

b) Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\: \: \)\(\Rightarrow\dfrac{1}{20}=\dfrac{1}{40}+\dfrac{1}{d'}\:\)
\(\Rightarrow\dfrac{1}{d'}=\dfrac{1}{20}-\dfrac{1}{40}\)
\(\Rightarrow d'=40\) (cm)
c) Chiều cao của ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\) \(\Rightarrow\dfrac{10}{h'}=\dfrac{40}{40}\)
\(\Rightarrow h'=10\) (cm)

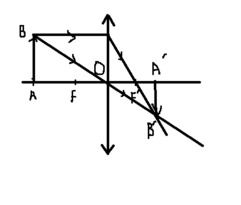
a)Ảnh A'B' là ảnh thật, ngược chiều vật và bằng vật (Hình vẽ tương đối đúng).
b)Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{10}=\dfrac{1}{20}+\dfrac{1}{d'}\)
\(\Rightarrow d'=20cm\)
Chiều cao ảnh: \(\dfrac{h}{h'}=\dfrac{d}{d'}\)
\(\Rightarrow\dfrac{2}{h'}=\dfrac{20}{20}\Rightarrow h'=2cm\)

Đáp án cần chọn là: D
Ta có công thức thấu kính:
1 d + 1 d ' = 1 f ⇒ 1 20 + 1 d ' = 1 10 ⇒ d ' = 20 c m

a, áp dụng công thức thấu kính hội tụ cho ảnh thật
theo bài ra\(=>f=5cm,d=10cm,h=3cm\)
\(=>\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}< =>\dfrac{1}{5}=\dfrac{1}{10}+\dfrac{1}{d'}=>d'=10cm\)
\(=>\dfrac{h}{h'}=\dfrac{d}{d'}=>\dfrac{3}{h'}=\dfrac{10}{10}=>h'=3cm\)
b, ý là: dịch A ra xa thấu kính 4 lần so với vị trí ở ý a hả chị?
\(=>d=4.10=40cm\)
\(=>\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}< =>\dfrac{1}{f}=\dfrac{1}{40}+\dfrac{1}{125}=>f=30cm\)

Đáp án: A
Ảnh S' là ảnh thật
Áp dụng công thức:
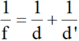
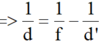
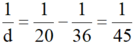
=> d = 45 cm
Vậy để thu được ảnh S' là ảnh thật và cách thấu kính 36cm thì khoảng cách từ vật đến thấu kính là 45cm
Đáp án A