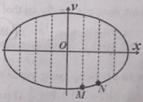
Một vật dao động điều hòa. Hình bên là đồ thị biểu diễn mối quan hệ giữa vận tốc v và li độ x của vật. Gọi k 1 , k 2 lần lượt là hệ số góc của tiếp tuyến với đồ thị tại M và N. tỷ số k 1 k 2 bằng
A. 1 5
B. 2 7
C. 1 6
D. 2 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
+ Ta có phương trình độc lập thời gian giữa v và x là elip có dạng: x 2 A 2 + v 2 ( ω A ) 2 = 1
+ Gọi chiều dài 1 ô là n, theo định nghĩa elip, ta có:
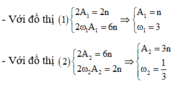
+ Theo đề bài: Lực kéo về cực đại tác dụng lên hai vật trong quá trình dao động là bằng nhau nên:
k 1 A 1 = k 2 A 2 ⇔ m 1 ω 1 2 A 1 = m 2 ω 2 2 A 2
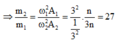

Chọn C
Cực kéo về cực đại tác dụng lên hai vật trong quá trình dao động là bằng nhau.
ðF=k|x|=> F m a x =k.A=m ω 2 A
ð m 1 2 ω 1 2 A 1 = m 1 2 ω 1 2 A 2 => m 1 m 2 = ω 1 2 A 1 ω 2 2 A 2
ð = m 1 2 ω 1 2 A 2
Theo đồ thị:
+ Độ dài trục lớn elip = 2a
+ Độ dài trục bé elip =2b
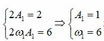
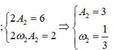
ð m 1 m 2 =27

Đáp án là C
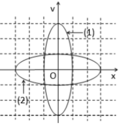
Cực kéo về cực đại tác dụng lên hai vật trong quá trình dao động là bằng nhau.
ð F=k|x|=> Fmax=k.A=mw2A
ð m1ω21A1=m2ω22A2=>m1m2=ω21.A1ω22.A2
ð 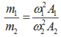
Theo đồ thị:
+ Độ dài trục lớn elip = 2a
+ Độ dài trục bé elip =2b
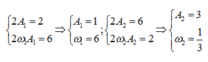

+ Nhìn vào đồ thị ta thấy: A 2 = 3 A 1 ⇒ A 2 = v 1 max = A 1 ω 1 A 1 = v 2 max = A 2 ω 2 ⇒ ω 1 ω 2 = A 2 2 A 1 2 1
+ Theo giải thiết: k 1 A 1 = k 2 A 2 ⇒ m 1 ω 1 2 A 1 = m 2 ω 2 2 A 2 ⇒ m 2 m 1 = ω 1 2 ω 2 2 A 1 A 2 2
→ Từ (1) và (2) m 2 m 1 = A 1 A 2 2 = 27
Chọn đáp án C

Đáp án C
Trên đồ thị ta thấy: A 2 = 3 A 1 ; v 1 m a x = 3 v 2 m a x , do đó:

= 3.3 = 9
Theo đề: 
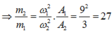
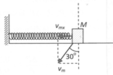

Đáp án C
+ Ta có phương trình độc lập thời gian giữa v và x là elip có dạng: 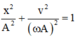
+ Gọi chiều dài 1 ô là n, theo định nghĩa elip, ta có:
- Với đồ thị 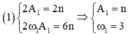
- Với đồ thị 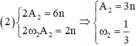
+ Theo đề bài: Lực kéo về cực đại tác dụng lên hai vật trong quá trình dao động là bằng nhau nên: ![]()
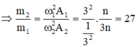

Đáp án C
Quy ước rằng 1 đơn vị trục hoành ứng với n, 1 đơn vị trục tung ứng với n’. Từ đồ thị ta thấy:
+ Vật (1): A 1 = n v 1 max = A 1 ω 1 = 3 n ' ⇒ ω 1 = 3 n ' n
+ Vật (2): A 2 = 3 n v 2 max = A 2 ω 2 = n ' ⇒ ω 2 = n ' 3 n
Có F k v 1 max = F k v 2 max ⇒ k 1 A 1 = k 2 A 2 ⇒ m 1 ω 1 2 A 1 = m 2 ω 2 2 A 2
⇒ m 2 m 1 = ω 1 2 A 1 ω 2 2 A 2 = 9 n ' 2 n 2 . n n ' 2 9 n 2 .3 n = 27