Cho hàm số
y
=
2
x
+
1
x
+
1
(C), gọi I là tâm đối xứng của đồ thị (C) và M(a;b) là một điểm thuộc đồ thị. Tiếp tuyến của đồ thị (C) tại điểm M cắt hai tiệm cận của đồ thị (C) lần lượt tại hai điểm A và B. Để tam giác IAB có bán kính đường tròn nội tiếp lớn nhất thì tổng a+b gần nhất với số nào sau đây? A. -3. B. 0. C. 3....
Đọc tiếp
Cho hàm số y = 2 x + 1 x + 1 (C), gọi I là tâm đối xứng của đồ thị (C) và M(a;b) là một điểm thuộc đồ thị. Tiếp tuyến của đồ thị (C) tại điểm M cắt hai tiệm cận của đồ thị (C) lần lượt tại hai điểm A và B. Để tam giác IAB có bán kính đường tròn nội tiếp lớn nhất thì tổng a+b gần nhất với số nào sau đây?
A. -3.
B. 0.
C. 3.
D. 5.
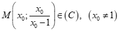
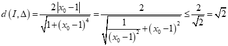
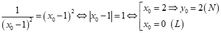
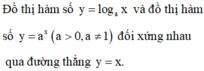
Đáp án B
Tâm đối xứng của đồ thị (C) là giao điểm hai đường tiệm cận. (C) có tiệm cận đứng là x=-1, tiệm cận ngang là y=2 => I(-1;2)
Ta có: y ' = 1 x + 1 2 ⇒ PTTT tại điểm M a ; b là y = 1 a + 1 2 x − a + 2 a + 1 a + 1 . Từ đây ta xác định được giao điểm của PTTT tại M a ; b và hai tiệm cận x = − 1 , y = 2 là A − 1 ; 2 a a + 1 , B 2 a + 1 ; 2 .
Độ dài các cạnh của Δ I A B như sau
I A = 2 a a + 1 − 2 = 2 a + 1 I B = 2 a + 1 + 1 = 2 a + 1 A B = 2 1 a + 1 2 + a + 1 2 ⇒ S I A B = 1 2 I A . I B = 2 ;
P = I A + I B + A B 2 = 1 a + 1 + a + 1 + 1 a + 1 2 + a + 1 2
Áp dụng bất đẳng thức Cosi ta có p ≥ 2 + 2 đạt được ⇔ a + 1 = 1 ⇔ a = 0 ⇒ b = 1 a = − 2 ⇒ b = 3 ⇒ a + b = 1