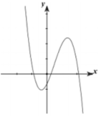
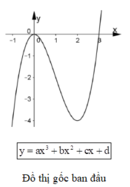
Cho hàm số y=ax3 + bx2 + cx + d có đồ thị như hình bên.
Trong các giá trị a,b,c,d có bao nhiêu giá trị âm?
A. 3
B. 1
C. 2
D. 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


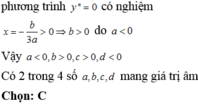

Chọn A
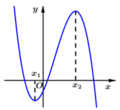
Qua đồ thị ta thấy: đồ thị hàm số ![]() giao với trục Oy tại điểm D(0;d) nằm phía dưới trục Ox nên d < 0, và hình dạng của đồ thị hàm số ứng với trường hợp a < 0.
giao với trục Oy tại điểm D(0;d) nằm phía dưới trục Ox nên d < 0, và hình dạng của đồ thị hàm số ứng với trường hợp a < 0.
Hàm số đạt cực tiểu tại x 1 < 0, đạt cực đại tại x 2 > 0 và x 1 + x 2 > 0. x 1 , x 2 là hai nghiệm của phương trình
![]() Khi đó:
Khi đó:
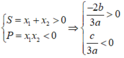
mà a < 0 nên: 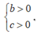
Vậy có 2 giá trị âm trong các giá trị a,b,c,d là 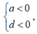

Ta có thể vẽ đồ thị hàm số y = |ax3+ bx2+ cx+ d + 1| theo ba bước sau:
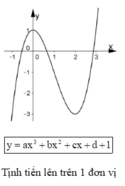
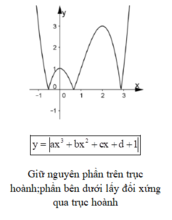
Dựa vào đồ thị ta thấy hàm số có 4 cực trị
Chọn C.

Có đa thức a x 3 + b x 2 + c x + d bậc ba có ba nghiệm x 1 = 1 , x 2 = 3 , x 3 = 5
Vì vậy a x 3 + b x 2 + c x + d = a x - 1 x - 3 x - 5
Diện tích tô đậm
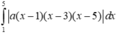
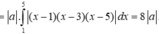
Theo giải thiết có ![]()
Vì ![]()
Vậy a x 3 + b x 2 + c x + d
![]()
Thay x=-1 vào hai vế đẳng thức có
![]() a-b+c-d=6
a-b+c-d=6
Chọn đáp án C.

Đáp án C
Phương pháp : Xác định hàm số f’(x) từ đó tính được ![]()
Cách giải : Ta dễ dàng tìm được phương trình parabol là
![]()
![]()
Đồ thị hàm số đi qua gốc tọa độ ![]()
![]()