Gọi(T) là tiếp tuyến của đồ thị
y
=
x
+
1
x
+
2
C
tại điểm có tung độ dương, đồng thời (T)cắt hai tiệm của (C) lần lượt tại A và B sao cho độ dài AB nhỏ nhất. Khi đó (T) tạo với hai trục tọa độ một tam giác có diện tích bằng bao nhiêu? A. 0,5 B. 2,5 C. 12,5 ...
Đọc tiếp
Gọi(T) là tiếp tuyến của đồ thị y = x + 1 x + 2 C tại điểm có tung độ dương, đồng thời (T)cắt hai tiệm của (C) lần lượt tại A và B sao cho độ dài AB nhỏ nhất. Khi đó (T) tạo với hai trục tọa độ một tam giác có diện tích bằng bao nhiêu?
A. 0,5
B. 2,5
C. 12,5
D. 8
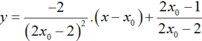
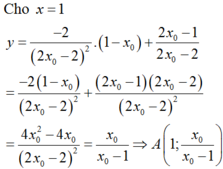
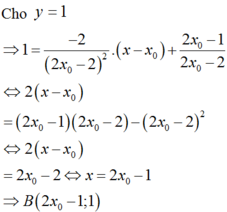
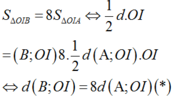
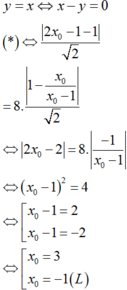
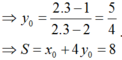
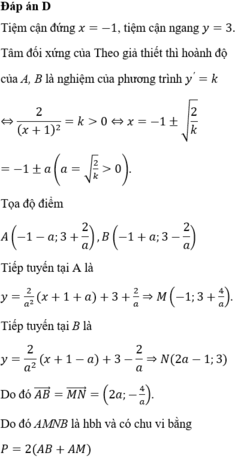
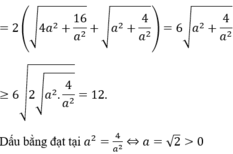
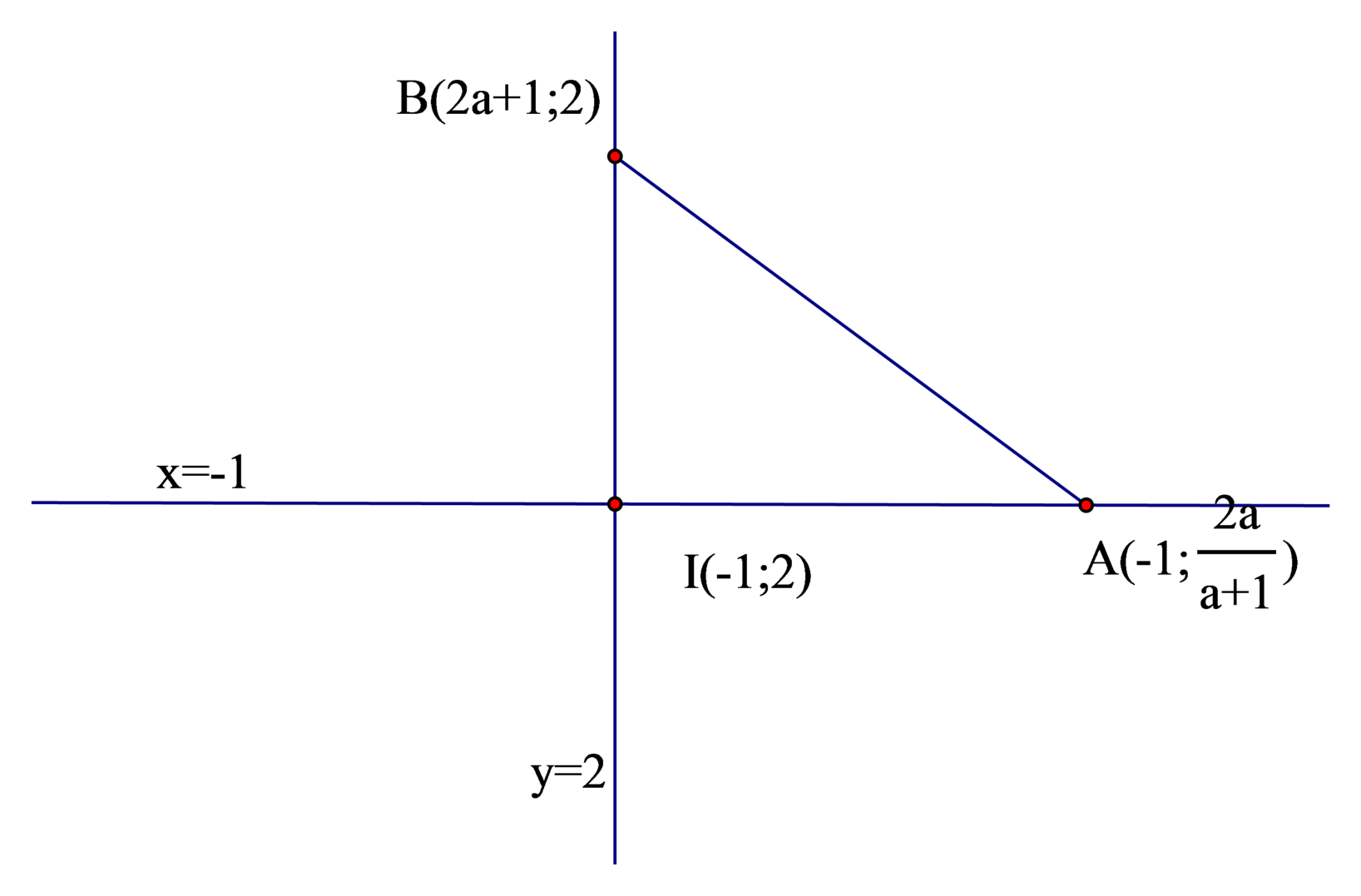
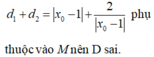
Đáp án C
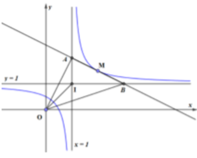
Gọi M a ; a + 1 a + 2 ∈ C ⇒ y ' a = 1 a + 2 2 nên phương trình tiếp tuyến của (C) tại M là
y = a + 1 a + 2 = 1 a + 2 2 x − a ⇔ y = x a + 2 2 + a 2 + 2 a + 2 a + 2 2 d
Đường thẳng (d) cắt TCĐ tại A − 2 ; a a + 2 ⇒ I A = 2 a + 2
Đường thẳng (d) cắt TCN tại B 2 a + 2 ; 1 ⇒ I B = 2 a + 2
Suy ra I A . I B = 4 mà A B 2 = I A 2 + I B 2 ≥ 2. I A . I B = 8 ⇒ A B ≥ 2 2
Dấu “=” xảy ra khi và chỉ khi 2 a + 2 = 2 a + 2 ⇔ a + 2 = 1 ⇒ a = − 1 a = − 3
Mà điểm M có tung độ dương ⇒ M − 3 ; 2 . Vậy d : y = x + 5 ⇒ S = 25 2 .