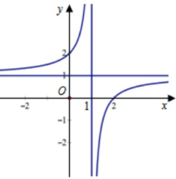
Cho hàm số f ( x ) = a x + b c x + d a , b , c , d ∈ R có đồ thị như hình vẽ bên. Tất cả các giá trị của m để phương trình |f(x)|=m có hai nghiệm phân biệt là
A. m ≥ 2 v à m ≤ 1
B. 0 < m < 1
C. m > 2 và m < 1
D. 0 < m < 1 và m > 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp : Xác định hàm số f’(x) từ đó tính được ![]()
Cách giải : Ta dễ dàng tìm được phương trình parabol là
![]()
![]()
Đồ thị hàm số đi qua gốc tọa độ ![]()
![]()

Điều kiện:


Từ đồ thị hàm số y=f(x) ta thấy phương trình f(x)=0 có nghiệm x=-3 (bội 2) và nghiệm đơn x = x 0 ∈ - 1 ; 0 nên ta viết lại f ( x ) = a x + 3 2 x - x 0
Khi đó

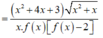
Dựa vào đồ thị ta cũng thấy, đường thẳng y=2 cắt đồ thị hàm số y=f(x) tại ba điểm phân biệt x=-1, x = x 1 ∈ - 3 ; - 1 , x = x 2 < - 3 nên ta viết lại
![]()
Khi đó
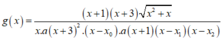
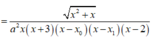
Dễ thấy x = x 0 ∈ - 1 ; 0 nên ta không xét giới hạn của hàm số tại điểm x 0
Ta có:
+) l i m x → 0 + g ( x ) = l i m x → 0 +
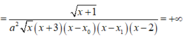
⇒ x = 0 là đường TCĐ của đồ thị hàm số y=g(x)
+) ![]()
⇒ Các đường thẳng x = - 3 , x = x 1 , x = x 2 đều là các đường tiệm cận đứng của đồ thị hàm số y=g(x)
Vậy đồ thị hàm số y=g(x) có tất cả 4 đường tiệm cận đứng.
Chọn đáp án D.

+ Ta có y ' = f ' ( x ) = a d - b c ( c x + d ) 2 . Từ đồ thị hàm số y= f’(x) ta thấy:
Đồ thị hàm số y= f’(x) có tiệm cận đứng x=1 nên –d/c= 1 hay c= -d
Đồ thị hàm số y= f’(x ) đi qua điểm (2;2)
⇒ a d - b c ( 2 c + d ) 2 = 2 ↔ a d - b c = 2 ( 2 c + d ) 2
Đồ thị hàm số y= f’(x) đi qua điểm (0;2)
⇒ a d - b c d 2 = 2 ↔ a d - b c = 2 d 2
Đồ thị hàm số y=f(x) đi qua điểm (0;3) nên b/d= 3 hay b= 3d
Giải hệ gồm 4 pt này ta được a=c= -d và b= 3d .
Ta chọn a=c= 1 ; b= -3 ; d= -1
⇒ y = x - 3 x - 1
Chọn D.
Đồ thị hàm số |f(x)| được suy ra từ đồ thị hàm số f(x) bằng cách:
Giữ nguyên phần đồ thị hàm số f(x) phía trên trục hoành;
Lấy đối xứng qua trục hoành phần đồ thị phía dưới trục hoành của hàm số f(x)
Quan sát đồ thị suy ra phương trình |f(x)=m có hai nghiệm thực phân biệt
Chọn đáp án D.