Cho hai số phức z 1 , z 2 có điểm biểu diễn lần lượt là M 1 , M 2 cùng thuộc đường tròn có phương trình x 2 + y 2 = 1 và z 1 - z 2 = 1 . Tính giá trị biểu thức P = z 1 + z 2
A. P = 3 2
B. P = 2
C. P = 2 2
D. P = 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
M 1 , M 2 thuộc đường tròn (T) có tâm O(0;0) và bán kính R=1

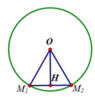

Đáp án D
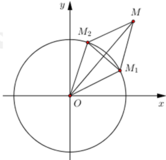
Tập hợp điểm biểu diễn số phức z 1 , z 2 là đường tròn tâm O, R = 1
Gọi M 1 z 1 , M 2 z 2 ⇒ O M 1 = O M 2 = 1
Ta có z 1 − z 2 = O M 1 → − O M 2 → = M 1 M 2 → = 1 ⇒ Δ O M 1 M 2 đều
Mà z 1 + z 2 = O M 1 → + O M 2 → = O M → = O M với M là điểm thỏa mãn O M 1 M M 2 là hình thoi cạnh 1 ⇒ O N = 3 ⇒ P = 3

Đáp án C
w = 1 − i z ⇒ i z = 1 − w ⇒ z = 1 − w i = − i + i w
z + i = 2 ⇔ − i + i w + i = 2 ⇔ i w = 2 ⇔ i w = 2 ⇔ w = 2
Vậy tập hợp các số phức w là đường tròn tâm O 0 ; 0 và bán kính R = 2 .

giải pt ta có
\(\begin{cases}z=2+\sqrt{5i}\\z=2-\sqrt{5}i\end{cases}\)
===> 2 điểm M,N lần lượt là M( 2, \(\sqrt{5}\)) VÀ N(2,-\(\sqrt{5}\))
MN=\(\sqrt{\left(2-2\right)^2+\left(-\sqrt{5}-\sqrt{5}\right)^2}\)=2\(\sqrt{5}\)