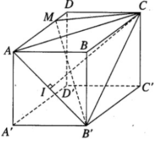
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AA'=2a, AD=4a.Gọi M là trung điểm của cạnh AD. Tính khoảng cách d từ giữa hai đường thẳng A’B’ và C’M
A. d = 2 a 2
B. d = a 2
C. d = 2 a
D. d = 3 a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Chọn hệ trục tọa độ như hình vẽ
A'(0;0;0), B'(4a;0;0), C'(4a;4a;0), M'(0;2a;2a)
A ' B ' → 4 a ; 0 ; 0 , C ' M → - 4 a ; - 2 a ; 2 a ⇒ A ' B ' → , C ' M → = 0 ; - 8 a 2 ; - 8 a 2 A ' M → 0 ; 2 a ; 2 a d ( A ' B ' , C ' M ) = A ' B ' → , C ' M → A ' M A ' B ' → , C ' M → = 32 a 3 8 2 a 2 = 2 2 a
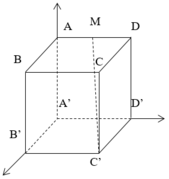

Đáp án A
Chọn hệ trục tọa độ như hình vẽ
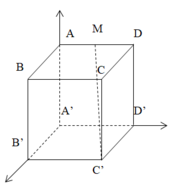
A ' ( 0 ; 0 ; 0 ) , B ' ( 4 a ; 0 ; 0 ) , C ' ( 4 a ; 4 a ; 0 ) , M ( 0 ; 2 a ; 2 a ) A ' B ' → ( 4 a ; 0 ; 0 ) , C ' M → ( − 4 a ; − 2 a ; 2 a ) ⇒ [ A ' B ' → , C ' M → ] = ( 0 ; − 8 a 2 ; − 8 a 2 ) A ' M → ( 0 ; 2 a ; 2 a ) d ( A ' B ' , C ' M ) = [ A ' B ' → , C ' M → ] A ' M → [ A ' B ' → , C ' M → ] = 32 a 3 8 2 a 2 = 2 2 a

Đáp án D
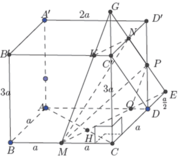
Gọi E là giao điểm của NP và CD. Gọi G là giao điểm của NP và CC’. Gọi K là giao điểm của MG và B’C’. Gọi Q là giao điểm của ME và AD. Khi đó mặt phẳng (MNP) chính là mặt phẳng (MEG). Gọi d 1 , d 2 lần lượt là khoảng cách từ C, A đến mặt phẳng (MEG). Do AC cắt (MEG) tại điểm H (như hình vẽ) nên d 1 d 2 = H C H A . Do tứ diện CMEG là tứ diện vuông tại C nên
1 d 1 2 = 1 C M 2 + 1 C E 2 + 1 C G 2
Ta có G C ' G C = C ' N C E = 1 3
Suy ra G C = 3 2 C C ' = 9 a 2
Như vậy: 1 d 1 2 = 1 a 2 + 4 9 a 2 + 4 81 a 2
Từ đó d 1 2 = 81 a 2 12 ⇒ d 1 = 9 11 . Ta có Q D M C = E D E C = 1 3 ⇒ Q D = a 3
Ta có Δ H C M đồng dạng với Δ H A Q nên:
H C H A = M C A Q = a 2 a − a 3 = 3 5 ⇒ d 1 d 2 = 3 5 ⇒ d 2 = 5 3 d 1 = 5.9 a 3.11 = 15 a 11

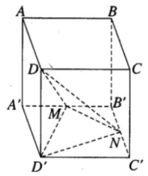
Thể tích khối chóp D’.DMN bằng thể tích khối chóp D.D’MN
Ta có: S D ' MN = S A ' B ' C ' D ' - S D ' A ' M + S D ' C ' N + S B ' MN
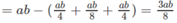
Thể tích khối chóp
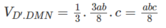
Từ đó suy ra tỷ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’ bằng 1/8

Gọi h là khoảng cách từ M đến mặt phẳng (AB’C)
Khi đó
![]()
Vì AC 2 = B ' C 2 = 5 a 2 nên tam giác ACB’ cân tại C. Do đó, đường trung tuyến CI của tam giác ACB’ cũng là đường cao.
Ta có:
![]()
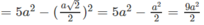
Do đó
![]()
Từ đó suy ra
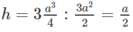
Đáp án A
Giả sử AB = x
B ' ( 0 ; 0 ; 0 ) , A ' ( x ; 0 ; 0 ) , C ' ( 0 ; 4 a ; 0 ) , M ( x ; 2 a ; 2 a ) A ' B ' → ( x ; 0 ; 0 ) , C ' M → ( x ; − 2 a ; 2 a ) , B ' C ' → ( 0 ; 4 a ; 0 ) [ A ' B ' → , C ' M → ] = ( 0 ; − 2 a x ; − 2 a x ) d ( A ' B ' ; C ' M ) = [ A ' B ' → , C ' M → ] B ' C ' → [ A ' B ' → , C ' M → ] = − 8 a 2 x 8 a 2 x 2 = 2 2 a