Cho tam giác ABC vuông cân tại A có BC= . Tính
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

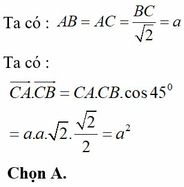

A C B D E H
Xét 2 tam giác AEC và tam giác HEB có:
\(\widehat{AEC}=\widehat{HEB}\left(=90^o\right)\)
AC=BH (giả thiết)
\(\widehat{CAE}=\widehat{BHE}\left(=\widehat{DHC}\right)\)
\(\Rightarrow\Delta AEC=\Delta HEB\left(ch.gn\right)\)
=> EC=EB (2 cạnh tương ứng)
=> tam giác ECB cân tại E
=> \(\widehat{B}=45^o\)
Đây chỉ là TH góc B nhọn, còn TH góc B tù thì làm tương tự tìm ra góc B=135 độ
O A B D H y x
Lấy B thuộc Ox , A thuộc Oy sao cho OA=OB
Dùng compa vẽ đtron (O;OB) và (B;OB), 2 đường tròn cắt nhau tại D ,nối O với D
Dùng compa vẽ đtron (D;R) và (B;R) (với R là bán kính bất kì), 2 đtron cắt nhau tại H, nối O với H
OD và OH chia góc ra làm 3 phần bằng nhau

(Bạn tự vẽ hình giùm)
a/ Ta có BA = BD (gt)
nên \(\Delta BAD\)cân tại B
=> \(\widehat{BAD}=\frac{180^o-\widehat{B}}{2}\)
=> \(\widehat{BAD}=\frac{180^o-60^o}{2}\)
=> \(\widehat{BAD}=\widehat{BDA}=60^o=\widehat{B}\)
=> \(\Delta BAD\)đều (đpcm)
b/ \(\Delta ABI\)và \(\Delta DBI\)có: AB = DB (gt)
\(\widehat{ABI}=\widehat{IBD}\)(BI là tia phân giác \(\widehat{B}\))
Cạnh BI chung
=> \(\Delta ABI\)= \(\Delta DBI\)(c. g. c) => \(\widehat{A}=\widehat{BDI}=90^o\)(hai cạnh tương ứng)
và AI = DI (hai cạnh tương ứng)
=> BI = IC (quan hệ giữa đường xiên và hình chiếu)
nên \(\Delta BIC\)cân tại I (đpcm)
c/ Ta có \(\Delta BIC\)cân tại I (cmt)
=> Đường cao ID cũng là đường trung tuyến của \(\Delta BIC\)
=> D là trung điểm BC (đpcm)
d/ Ta có \(\Delta ABC\)vuông tại A
=> BC2 = AB2 + AC2 (định lý Pythagore)
=> AB2 + AC2 = 262 = 676
và \(\frac{AB}{AC}=\frac{5}{2}\)=> \(\frac{AB}{5}=\frac{AC}{2}\)=> \(\frac{AB^2}{25}=\frac{AC^2}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{AB^2}{25}=\frac{AC^2}{4}=\frac{AB^2+AC^2}{25+4}=\frac{676}{29}\)
=> \(\hept{\begin{cases}\frac{AB}{5}=\frac{676}{29}\\\frac{AC}{2}=\frac{676}{29}\end{cases}}\)=> \(\hept{\begin{cases}AB=\frac{676}{29}.5\\AC=\frac{676}{29}.2\end{cases}}\)=> \(\hept{\begin{cases}AB=\frac{3380}{29}\left(cm\right)\\AC=\frac{1352}{29}\left(cm\right)\end{cases}}\)

Bạn nào trả lời được thì xin hãy giúp tớ luôn mai tớ phài nộp rồi nhưng tuần này nghỉ tết sức khỏe ko tốt ko đc đi đâu chơi chỉ ở nhà nằm nghỉ đc thôi. Bạn nào trả lời nhanh nhất tớ tích cho
2/
Ta có (x2 + 4) (x - 1) = 0
=> \(\orbr{\begin{cases}x^2+4=0\\x-1=0\end{cases}}\)=> \(\orbr{\begin{cases}x^2=4\\x=1\end{cases}}\)=> \(\orbr{\begin{cases}x=2\\x=1\end{cases}}\)
Thay x = 2 vào biểu thức B, ta có:
B = 3x2 + 8x - 1 = 3. 22 + 8.2 - 1 = 3.4 + 8.2 - 1 = 12 + 16 - 1 = 27
Thay x = 1 vào biểu thức B, ta có:
B = 3x2 + 8x - 1 = 3.12 + 8.1 - 1 = 3 + 8 - 1 = 11
Vậy khi (x2 + 4) (x - 1) = 0 thì giá trị của biểu thức B là 27 hoặc 11.

#)Giải :
a)\(\Delta ABC\)vuông tại A (gt) \(\Rightarrow\widehat{BAD}+\widehat{DAC}=90^o\left(1\right)\)
\(\Delta HAD\)vuông tại H (gt)\(\Rightarrow\widehat{HDA}+\widehat{HAD}=90^o\left(2\right)\)
Vì AD là tia phân giác của \(\widehat{HAC}\Rightarrow\)\(\widehat{HAD}=\widehat{DAC}\left(3\right)\)
Từ \(\left(1\right)\left(2\right)\left(3\right)\Rightarrow\widehat{BAD}=\widehat{DAC}\)
\(\Rightarrow\Delta ABD\)cân tại A
b) Từ cmt \(\Rightarrow AB=BD\)(tính chất của tam giác cân)
Đặt \(AB=BD=x\)
Áp dụng hệ thức lượng trong tam giác vuông ABC
\(\Rightarrow AB^2=HB.HC\)
Hay \(x^2=\left(x-6\right)25\)
\(\Rightarrow x^2-25+150=0\)
\(\Rightarrow\left(x-10\right)\left(x-15\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-10=0\\x-15=0\end{cases}\Rightarrow\orbr{\begin{cases}x=10\\x=15\end{cases}}}\)
Vậy AB = 10 hoặc AB = 15

Đường thẳng d bất kì đi qua A nên d có thể có các vị trí sau:
+) d không cắt cạnh BC.
A B C H E d
Trong tam giác vuông AHB có: góc HAB + ABH = 900 (1)
Mà góc HAB + BAC + CAE = 180o => góc HAB + CAE = 180o - BAC = 180 - 90 = 90o (2)
(1)(2) => góc ABH = CAE
tam giác vuông ABH = CAE ( do cạnh huyền AB = AC; góc ABH = CAE)
=> AH = CE
*) Áp dụng định lí Pi ta go trong tam giác vuông ABH có: BH2 + AH2 = AB2
mà AH = CE nên BH2 + CE2 = BH2 + AH2 = AB2
Dễ có: AB2 + AC2 = BC2 ; AB = AC => 2.AB2 = a2 => AB2 = a2/ 2
Vậy BH2 + CE2 = a2/ 2
+) Khi d trùng với AB :
A B C d
=> H trùng với B; E trùng với A=> BH = 0; CE = CA
=> BH2 + CE2 = AC2 = a2/ 2
+) d trùng với AC (tương tự như d trùng với AB)
+) Khi d cắt cạnh BC:
A B C d H E
*) Ta cũng chứng minh : tam giác AEC = BHA (cạnh huyền - góc nhọn)
=> BH = AE
*) Trong tam giác vuông AEC có: AE2 + CE2 = AC2
=> BH2 + CE2 = AE2 + CE2 = AC2 = a2/ 2
Vậy BH2 + CE2 = AC2 = a2/ 2

Sửa đề: cắt AB tại D.
a) Sửa đề: ΔACD=ΔECD
Xét ΔACD vuông tại A và ΔECD vuông tại E có
CD chung
\(\widehat{ACD}=\widehat{ECD}\)(CD là tia phân giác của \(\widehat{ACE}\))
Do đó: ΔACD=ΔECD(Cạnh huyền-góc nhọn)
b) Ta có: ΔACD=ΔECD(cmt)
nên DA=DE(Hai cạnh tương ứng)
Xét ΔDAE có DA=DE(cmt)
nên ΔDAE cân tại D(Định nghĩa tam giác cân)
 Bài 1. Cho tam giác ABC cân tại A có Â = 80o
Bài 1. Cho tam giác ABC cân tại A có Â = 80o