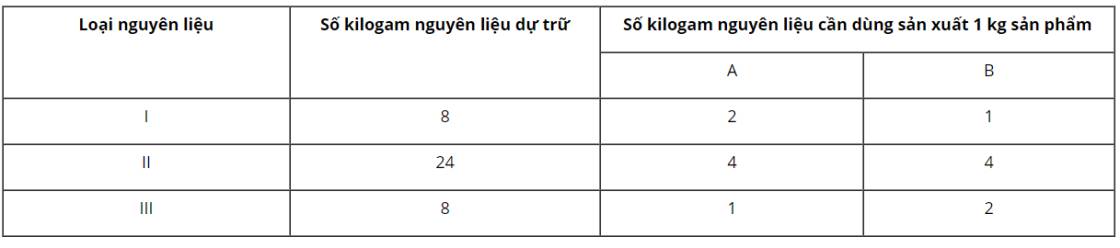
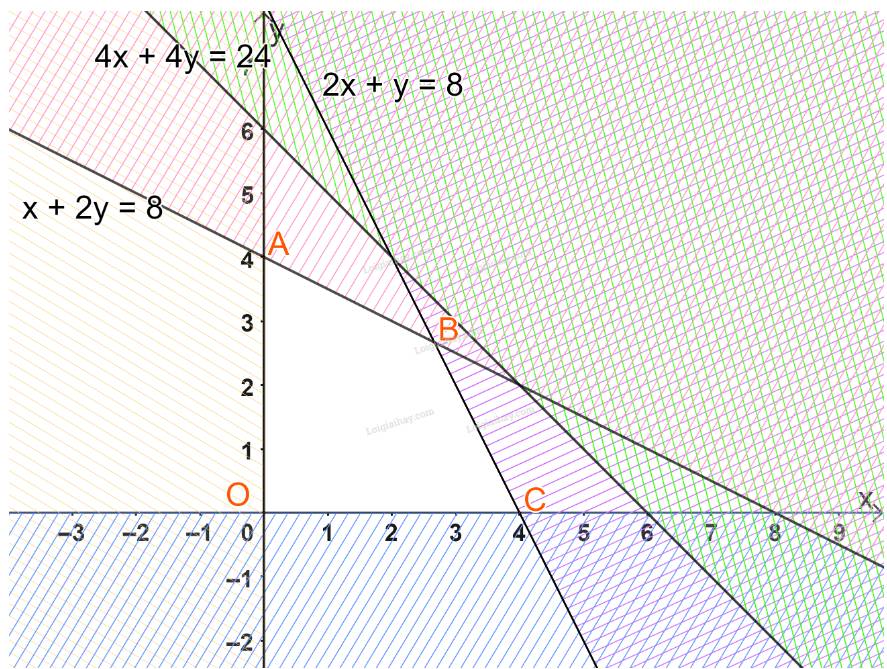
Công ty Bao bì Dược cần sản xuất 3 loại hộp giấy: đựng thuốc B 1 , đựng cao Sao vàng và đựng “Quy sâm đại bổ hoàn”. Để sản xuất các loại hộp này, công ty dùng các tấm bìa có kích thước giống nhau. Mỗi tấm bìa có hai cách cắt khác nhau
- Cách thứ nhất cắt được 3 hộp B 1 , một hộp cao Sao vàng và 6 hộp Quy sâm
- Cách thứ hai cắt được 2 hộp B 1 , 3 hộp cao Sao vàng và 1 hộp Quy sâm. Theo kế hoạch, số hộp Quy sâm phải có là 900 hộp, số hộp B 1 tối thiểu là 900 hộp, số hộp cao Sao vàng tối thiểu là 1000 hộp. Cần phương án sao cho tổng số tấm bìa phải dùng là ít nhất?
A. Cắt theo cách một x - 2 < 0 tấm, cắt theo cách hai 300 tấm
B. Cắt theo cách một 150 tấm, cắt theo cách hai 100 tấm
C. Cắt theo cách một 50 tấm, cắt theo cách hai 300 tấm
D. Cắt theo cách một 100 tấm, cắt theo cách hai 200 tấm


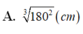
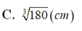
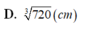


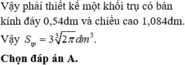
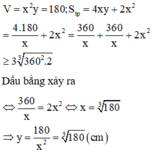
Chọn đáp án A