Nghiệm của phương trình tan ( 2 x - 15 ° ) = 1 , với - 90 ° < x < 90 ° là
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

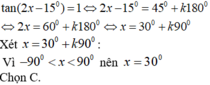

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

Ta có: điều kiện xác định của bpt \(x+3-\dfrac{1}{x+7}< -\dfrac{1}{x+7}\) là \(x\ne-7\)
\(\Rightarrow x=-7\) không phải là nghiệm của bpt trên
Lại có: \(x+3< 2\\ \Leftrightarrow x< 2-3\\ \Leftrightarrow x< -1\)
\(\Rightarrow x=-7\) thỏa mãn bpt \(x+3< 2\) \(\left(-7< -1\right)\)

Thay x = -2 vào pt trên ta đc
\(\left(-2\right)^2-\left(2m+1\right)\left(-2\right)+m^2+m=0\)
\(4+4m-2+m^2+m=0\)
\(m^2+5m+2=0\)
Ta có : \(5^2-4.2=25-8=17>0\)
Suy ra : \(m_1=\frac{-5-\sqrt{17}}{2};m_2=\frac{-5+\sqrt{17}}{2}\)
Mà cho luôn vô nghiệm đi cho nhanh.

28.
\(tan\left(2x-15^0\right)=1\Leftrightarrow2x-15^0=45^0+k180^0\)
\(\Leftrightarrow2x=60^0+k180^0\)
\(\Leftrightarrow x=30^0+k90^0\)
\(-90^0\le30^0+k90^0\le90^0\Rightarrow k=\left\{-1;0\right\}\)
\(\Rightarrow x=\left\{-60^0;30^0\right\}\Rightarrow\sum x=-30^0\)
34.
\(tan\left(x+\frac{\pi}{2}\right)=1\Leftrightarrow x+\frac{\pi}{2}=\frac{\pi}{4}+k\pi\)
\(\Rightarrow x=-\frac{\pi}{4}+k\pi\)
\(\Rightarrow sin\left(2x-\frac{\pi}{6}\right)=sin\left[2\left(-\frac{\pi}{4}+k\pi\right)-\frac{\pi}{6}\right]\)
\(=sin\left(-\frac{2\pi}{3}+k2\pi\right)=sin\left(-\frac{2\pi}{3}\right)=-\frac{\sqrt{3}}{2}\)

\(A=s\left(x\right)cs\left(x\right)+\frac{\left(s^3\left(x\right)+cs^3\left(x\right)\right)}{cs\left(x\right)\left(1+t\left(x\right)\right)}=s\left(x\right)cs\left(x\right)+\left(\frac{\left(s\left(x\right)+cs\left(x\right)\right)\left(1-s\left(x\right)cs\left(x\right)\right)}{\left(s\left(x\right)+cs\left(x\right)\right)}\right)\)
\(=1\) vì \(s\left(x\right)+cs\left(x\right)\ne0,\forall0< =x< =\frac{\pi}{2}\)

a) Ta có: \(\sin^2a^o=\cos^2\left(90^o-a^o\right)\)
Biểu thức trên
\(=\left(\sin^21^o+\sin^o89\right)+\left(\sin^22^o+\sin^288^o\right)+...+\left(\sin^244^o+\sin^246^o\right)+\sin^245^o\)
\(=\left(\sin^21^o+\cos^21^o\right)+\left(\sin^22^o+\cos^22^o\right)+...+\left(\sin^244^o+\cos^246^o\right)+\sin^245^o\)
\(=1+1+..+1+\sin^245^o=44+\frac{1}{2}=\frac{89}{2}\)
b)
Ta có: \(\sin^2x+\cos^2x=1\)
\(0^o< x< 90^o\)
=> \(0< \sin x;\cos x< 1\)
Ta có: \(\frac{\sin^2x+\cos^2x}{\text{}\text{}\sin x.\cos x}=\frac{1}{\frac{12}{25}}=\frac{25}{12}\Leftrightarrow\frac{\sin x}{\cos x}+\frac{\cos x}{\sin x}=\frac{25}{12}\)
\(\Leftrightarrow\tan x+\frac{1}{\tan x}=\frac{25}{12}\Leftrightarrow\tan^2x-\frac{25}{12}\tan x+1=0\)
Đặt t =tan x => có phương trình bậc 2 ẩn t => Giải đen ta => ra đc t => ra đc tan t
\(\Leftrightarrow\orbr{\begin{cases}\tan x=\frac{3}{4}\\\tan x=\frac{4}{3}\end{cases}}\)