Thu gọn rồi tìm bậc của đa thức x3 y4 - 5y8 + x3 y4 + xy4 + x3 - y2 - xy4 + 5y8.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Thu gọn đa thức
B(x) = x3y4 - 5y8 + x3y4 + xy4 + x3 - y2 - xy4 + 5y8
= 3x3y4 + x3 - y2
Bậc của đa thức là 7. Chọn B

\(A=\left(-\dfrac{2}{3}x^3y^4\right)^2.\left(-3x^5y^2\right)^3\)
\(A=\left(\dfrac{4}{9}x^6y^8\right).\left(-27x^{15}y^6\right)\)
\(A=\left(\dfrac{4}{9}.-27\right)\left(x^6.x^{15}\right)\left(y^8.y^{16}\right)\)
\(A=-12x^{21}y^{24}\)
\(\text{Hệ số:-12}\)
\(\text{Bậc:45}\)
\(B=\left(3x^2y\right).\left(-\dfrac{1}{3}x^3y\right).\left(-\dfrac{1}{4}x^3y^4\right)\)
\(B=\left(3.-\dfrac{1}{3}.-\dfrac{1}{4}\right).\left(x^2.x^3.x^3\right).\left(y.y.y^4\right)\)
\(B=\dfrac{1}{4}x^8y^6\)
\(\text{Hệ số:}\dfrac{1}{4}\)
\(\text{Bậc:14}\)

a) Thu gọn và sắp xếp:
\(P\left(x\right)=2x^3-9x^2+5-4x^3+7x\)
\(P\left(x\right)=\left(2x^3-4x^3\right)-\left(9x^2+2x^2\right)+7x+5\)
\(P\left(x\right)=-2x^3-11x^2+7x+5\)
b) Thay x=1 vào đa thức P(x) ta được:
\(P\left(x\right)=\left(-1\right)^4-\left(-1\right)^3-\left(-1\right)-2=1\)

Khi x = - 1; y = 1 thì xy = (-1).1= -1
Ta có: xy – x2y2 + x3y3 – x4y4 + x5y5 – x6.y6
= xy – (xy)2 + (xy)3 – (xy)4 + (xy)5 – (xy)6
= -1 – (-1)2 + (-1)3 – (-1)4 + (-1)5 - (-1)6
= -1 – 1 + (-1) – 1 + (-1) – 1
= - 6
Chọn đáp án D

1: \(=\dfrac{x-1}{x^2+x+1}+\dfrac{x+1}{x-1}\)
\(=\dfrac{x^2-2x+1+x^3+x^2+x^2+x+x+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^3+3x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}\)
2: \(=\dfrac{\left(x^2-y^2\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}=\dfrac{\left(x-y\right)\left(x+y\right)^2}{x^2+xy+y^2}\)
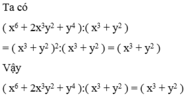
x3y4 - 5y8 + x3y4 + xy4 + x3 - y2 - xy4 + 5y8
= (x3y4 + x3y4) + (xy4 – xy4) + (-5y8 + 5y8) + x3 – y2
= (1+ 1)x3y4 + (1 – 1).xy4 + ( - 5+ 5)y8 + x3 – y2
= 2x3y4 + x3 - y2.
Đa thức có bậc là 7.