Cho a và b là hai đường thẳng chéo nhau. Có thể tính khoảng cách giữa hai đường thẳng chéo nhau này bằng những cách nào?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 9 2019
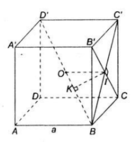
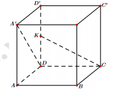
a) Ta có:
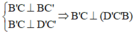
Gọi I là tâm hình vuông BCC'B'
Trong mặt phẳng (BC'D') vẽ IK ⊥ BD' tại K
Ta có IK là đường vuông góc chung của BD' và B'C
b) Gọi O là trung điểm của BD'
Tam giác BC’D’ có OI là đường trung bình nên :
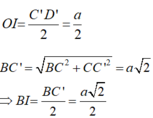
Vì ΔIOB vuông tại I có đường cao IK nên:
CM
28 tháng 6 2019
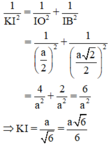
Đáp án D
Chọn hệ trục với D 0 ; 0 ; 0 , A a ; 0 ; 0 , A ' a ; 0 ; a , K 0 ; 0 ; a 2 , C 0 ; a ; 0
Khi đó D A ' → = a ; 0 ; a , K C → 0 ; a ; - a 2 ⇒ D A ' → ; K C → = a 2 2 2 ; - 1 ; - 2
Phương trình mặt phẳng qua C (chứa CK) và song song với DA’ là (P):2x - y - 2z + a = 0
Khi đó d C K ; A ' D = d D ; P = a 3 .
CM
30 tháng 1 2018
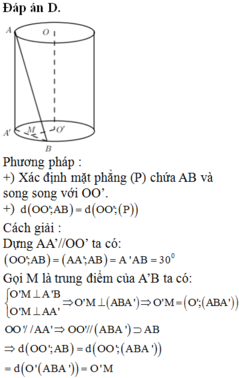
Đáp án D.
Phương pháp :
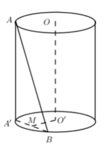
+) Xác định mặt phẳng (P) chứa AB và song song với OO’.
+) d(OO’;AB) = D(OO’;(P))
Cách giải :
Dựng AA’//OO’ ta có: (OO’;AB) = (AA’;AB) = A’AB = 300
Gọi M là trung điểm của A’B ta có:
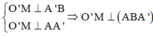
=>d(OO’;AB) = d(OO’;(ABA’)) = d(O’;(ABA’)) = O’M
Xét tam giác vuông ABA’ có 
Xét tam giác vuông O’MB có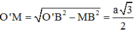 
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 2 2022
Do \(AB||CD\Rightarrow AB||\left(SCD\right)\Rightarrow d\left(AB;SC\right)=d\left(AB;\left(SCD\right)\right)=d\left(A;\left(SCD\right)\right)\)
Trong tam giác SAD, kẻ \(AH\perp SD\) \(\Rightarrow AH\perp\left(SCD\right)\)
\(\Rightarrow AH=d\left(A;\left(SCD\right)\right)\)
Tam giác SAD vuông cân tại A \(\Rightarrow AH=\dfrac{AD}{\sqrt{2}}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow d\left(SC;AB\right)=\dfrac{a\sqrt{2}}{2}\)
22 tháng 9 2023
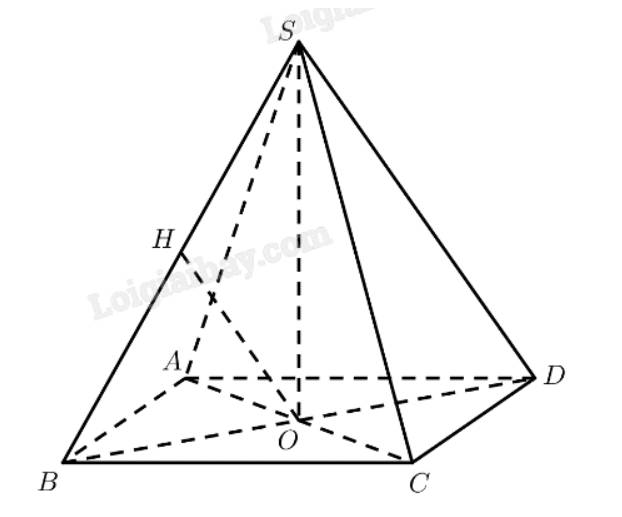
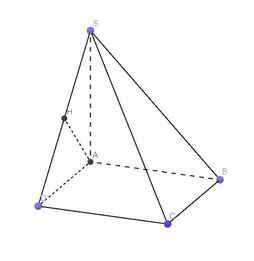
a) Kẻ \(OH \bot SB\left( {H \in SB} \right)\)
\(S.ABC{\rm{D}}\) là chóp tứ giác đều \( \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AC\)
\(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\( \Rightarrow AC \bot \left( {SB{\rm{D}}} \right) \Rightarrow AC \bot OH\)
Mà \(OH \bot SB\)
\( \Rightarrow d\left( {AC,SB} \right) = OH\)
\(B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2}} = a\sqrt 2 \Rightarrow BO = \frac{1}{2}B{\rm{D}} = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SBO\) vuông tại \(O \Rightarrow SO = \sqrt {S{B^2} - B{O^2}} = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SBO\) vuông cân tại \(O\) có đường cao \(OH\)
\( \Rightarrow d\left( {AC,SB} \right) = OH = \frac{1}{2}SB = \frac{a}{2}\)
b) \({S_{ABC{\rm{D}}}} = A{B^2} = {a^2}\)
\({V_{S.ABC{\rm{D}}}} = \frac{1}{3}{S_{ABC{\rm{D}}}}.SO = \frac{{{a^3}\sqrt 2 }}{6}\)
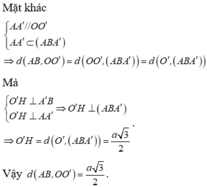
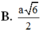
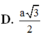
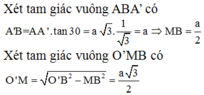
Có 2 cách để tính khoảng cách giữa hai đường thẳng chéo nhau