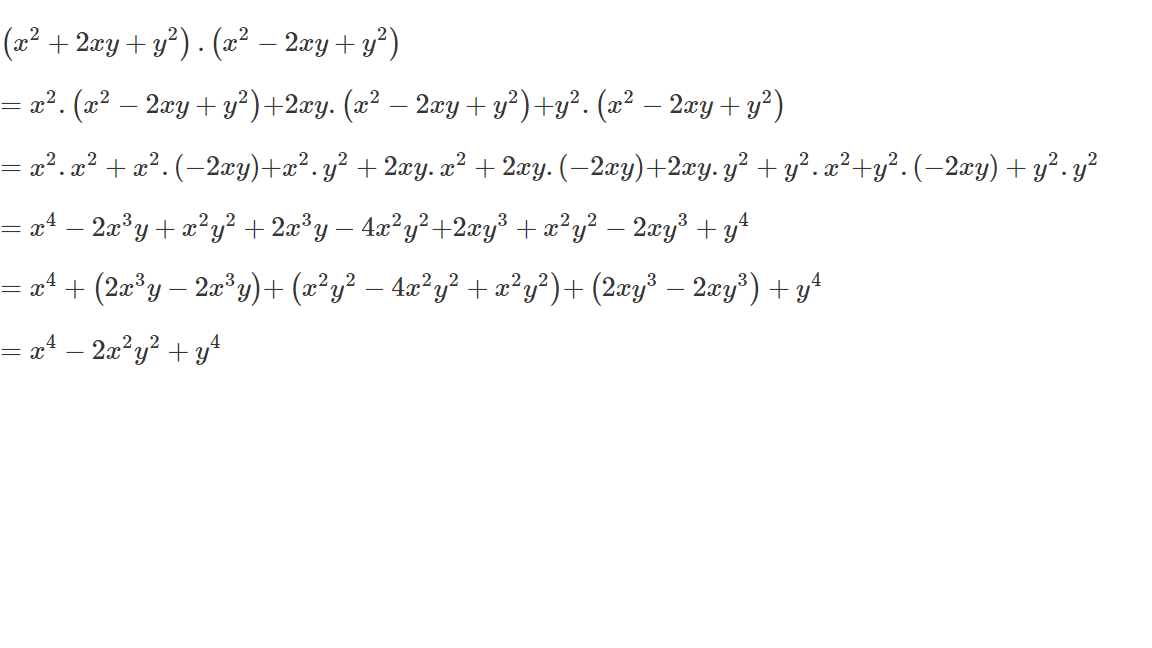X2+2XY+Y2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A=x2+y2-2xy-x2+y2+2xy
=x2-x2+y2+y2+2xy-2xy
=y4
vậy da thức A sau khithu gọn là: y4

a) \(x^2+2xy+y^2-4=\left(x+y\right)^2-2^2\)
\(=\left(x+y-2\right)\left(x+y+2\right)\)
b) \(x^2-y^2+x+y=\left(x-y\right)\left(x+y\right)+1\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y+1\right)\)
c) \(y^2+x^2+2xy-16=x^2+2xy+y^2-16\)
\(=\left(x+y\right)^2-4^2=\left(x+y+4\right)\left(x+y-4\right)\)

\(\left(x^2+2xy+y^2\right)\left(x^2-2xy+y^2\right)=\left(x-y\right)^2\cdot\left(x+y\right)^2=\left(x^2-y^2\right)^2=x^4-2x^2y^2+y^4\)

M – N = (x2 – 2xy + y2)– (y2 +2xy +x2 + 1)
= x2 – 2xy + y2 – y2 – 2xy – x2 – 1
= (x2– x2) + (y2 – y2) + (– 2xy – 2xy) – 1
= 0 + 0 – 4xy – 1
= – 4xy – 1.

M + N = (x2 – 2xy + y2)+ (y2 + 2xy + x2 + 1)
= x2 – 2xy + y2 + y2 + 2xy + x2 + 1
= (x2+ x2) + (y2 + y2) + (– 2xy+ 2xy) + 1
= 2x2 + 2y2 + 0 + 1
= 2x2 + 2y2 +1

a: \(\dfrac{x^2+2xy+y^2}{x+y}=x+y\)
b: \(\dfrac{64x^3+1}{4x+1}=16x^2-4x+1\)

a) \(\left(x^2+2xy+y^2\right):\left(x+y\right)=\left(x+y\right)^2:\left(x+y\right)=x+y\)
b) \(=\left[\left(5x+1\right)\left(25x^2-5x+1\right)\right]:\left(5x+1\right)=25x^2-5x+1\)
c) \(=\left(y-x\right)^2:\left(y-x\right)=y-x\)
\(a,=\left(x+y\right)^2:\left(x+y\right)=x+y\\ b,=\left(5x+1\right)\left(25x^2-5x+1\right):\left(5x+1\right)=25x^2-5x+1\\ c,=\left(y-x\right)^2:\left(y-x\right)=y-x\)

\(\dfrac{-x^2+2xy-y^2}{x+y}=\dfrac{-\left(x^2-2xy+y^2\right)}{x+y}=\dfrac{-\left(x-y\right)^2}{\left(x+y\right)}=\dfrac{-\left(x-y\right)^3}{\left(x+y\right)\left(x-y\right)}=\dfrac{-\left(x-y\right)^3}{x^2-y^2}=\dfrac{\left(x-y\right)^3}{y^2-x^2}\Rightarrow?=\left(x-y\right)^3\)
\(\dfrac{-x^2+2xy-y^2}{x+y}=\dfrac{?}{y^2-x^2}\)
\(\dfrac{-\left(x-y\right)^2}{x+y}=\dfrac{-?}{x^2-y^2}\)
\(\dfrac{-\left(x-y\right)^2}{x+y}=\dfrac{-?}{\left(x-y\right)\left(x+y\right)}\)
\(-?\left(x+y\right)=-\left(x-y\right)^3\left(x+y\right)\)
\(?=\left(x-y\right)^3\)