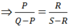Cho hai phân thức P Q v à R S
Chứng minh rằng :
Nếu P Q = R S và P ≠ S thì P Q - P = R S - R
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 6 2022
a: \(\dfrac{P}{Q}=\dfrac{R}{S}\)
nên \(\dfrac{P}{Q}+1=\dfrac{R}{S}+1\)
hay \(\dfrac{P+Q}{Q}=\dfrac{R+S}{S}\)
b: P/Q=R/S=k
=>P=Qk; R=Sk
\(\dfrac{P}{Q-P}=\dfrac{Qk}{Q-Q\cdot k}=\dfrac{k}{1-k}\)
\(\dfrac{R}{S-R}=\dfrac{S\cdot k}{S-S\cdot k}=\dfrac{k}{1-k}\)
Do đó: \(\dfrac{P}{Q-P}=\dfrac{R}{S-R}\)
29 tháng 4 2017
a)
\(\dfrac{P}{Q}=\dfrac{R}{S}\Rightarrow PS=QR\)
\(\Leftrightarrow PS+QS=QR+QS\)
\(\Leftrightarrow S\left(P+Q\right)=Q\left(R+S\right)\)
điều kiện Q,s khác 0 => chia hau vế cho QS
\(\Leftrightarrow\dfrac{S\left(P+Q\right)}{QS}=\dfrac{Q\left(R+S\right)}{QS}\Leftrightarrow\dfrac{\left(P+Q\right)}{Q}=\dfrac{\left(R+S\right)}{S}\) đpcm
4 tháng 11 2016
Bài này lớp 7 thôi mà !
a) Cộng 1 vào 2 vế
b) Nghịch đảo 2 vế,trừ 1 ở 2 vế rồi lại nghịch đảo 2 vế
5 tháng 11 2016
ta có P/Q = R/S => PS= RQ (1)
P/Q-P = R/S-R => P( S-R) = R(Q-P)
=> PS -PR = RQ-RP
từ (1) => P/Q-P= R/S-R (bn tự kết luận nhé
còn người ta cho Q khác P để Q-P khác 0 vì Q-P là mẫu số và R-S cũng vậy nên S khác R
PT
1
CM
5 tháng 5 2018
Xuất phát từ điều cần chứng minh Û P(S + R) = R(Q + P)
Rút gọn còn PS = RQ hay P Q = R S (đúng với giả thiết).
4 tháng 11 2017
Bài 1.
a) Do hai phân thức bằng nhau , ta có :
( x +2)P( x2 - 22) = ( x - 1)Q( x -2)
=( x + 2)P( x - 2)( x + 2) = ( x - 1)Q( x - 2)
Suy ra : P = x - 1 ; Q = ( x + 2)2
b) Do hai phân thức bằng nhau , ta có :
( x + 2)P(x2 - 2x + 1) = ( x - 2)Q( x2 - 1)
= ( x + 2)P( x - 1)2 = ( x - 2)Q( x - 1)( x + 1)
Suy ra : P = ( x - 2)( x + 1) = x2 - x - 2
Q = ( x + 2)( x - 1) = x2 + x + 2
4 tháng 11 2017
Bài 2. a) Do : \(\dfrac{P}{Q}=\dfrac{R}{S}=>PS=QR\)
Xét : ( P + Q)S= PS + QS = QR + QS = Q( R + S)
-> \(\dfrac{P+Q}{Q}=\dfrac{R+S}{S}\)
b) Do : \(\dfrac{P}{Q}=\dfrac{R}{S}=>PS=QR\)
Xét : ( S - R)P = PS - PR = QR - PR = R( Q - P)
-> \(\dfrac{R-S}{R}=\dfrac{Q-P}{P}\)
- > \(\dfrac{R}{R-S}=\dfrac{P}{Q-P}\)
Trừ từng vế đẳng thức (1) với PR: PS – PR = QR – PR
⇒ P(S – R) = R(Q – P)