Giải bất phương trình: 2x(6x - 1) > (3x - 2)(4x + 3)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KH
14 tháng 6 2021
a) \(\dfrac{15-6x}{3}>5\Leftrightarrow15-6x>15\)
\(\Leftrightarrow-6x>0\Leftrightarrow x< 0\) (vì \(-6< 0\))
\(S=\left\{x|x< 0\right\}\)
b) \(\dfrac{8-11x}{4}< 13\Leftrightarrow8-11x< 52\)
\(\Leftrightarrow-11x< -44\Leftrightarrow x>4\) (vì \(-11< 0\))
\(S=\left\{x|x>4\right\}\)
c) \(8x+3\left(x+1\right)>5x-\left(2x-6\right)\)
\(\Leftrightarrow8x+3x+1>5x-2x+6\)
\(\Leftrightarrow8x+3x-5x+2x>6-1\)
\(\Leftrightarrow8x>5\)
\(\Leftrightarrow x>\dfrac{5}{8}\) (vì \(8>0\))
\(S=\left\{x|x>\dfrac{5}{8}\right\}\)
d) \(2x\left(6x-1\right)>\left(3x-2\right)\left(4x+3\right)\)
\(\Leftrightarrow12x^2-2x>12x^2+9x-8x-6\)
\(\Leftrightarrow12x^2-2x-12x^2-9x+8x>-6\)
\(\Leftrightarrow-3x>-6\)
\(\Leftrightarrow x< 2\) (vì \(-3< 0\))
\(S=\left\{x|x< 2\right\}\)
SA
14 tháng 6 2021
a) \(\dfrac{15-6x}{3}>5\) <=> \(15-6x>15\) <=> \(6x< 0\) <=> \(x< 0\)
b) \(\dfrac{8-11x}{4}< 13\) <=> \(8-11x< 52\) <=> \(11x>-44\)<=> \(x>-4\)
c) \(8x+3\left(x+1\right)>5x-\left(2x-6\right)\)
<=> 8x + 3x + 3 - 5x + 2x - 6 > 0
<=> 8x > 3
<=> x > 3/8
d) 2x(6x - 1) > (3x - 2)(4x + 3)
<=> 12x2 - 2x > 12x2 + x - 6
<=> 12x2 - 2x - 12x2 - x > -6
<=> -3x > -6
<=> x < 2
5 tháng 4 2018
a) \(8x+3\left(x+1\right)>5x-\left(2x-6\right)\)
⇒ \(8x + 3x + 3 > 5x - 2x + 6\)
⇒ \(11x+3>3x+6\)
⇒ \(11x - 3x > 6 -3\)
⇒ \(8x > 3\)
⇒ \(8x.\dfrac{1}{8}>3.\dfrac{1}{8}\)
⇒ \(x>\dfrac{3}{8}\)
S = \(\left\{x\backslash x>\dfrac{3}{8}\right\}\)
b) \(2x(6x-1) > (3x -2)(4x+3)\)
⇒ \(12x^2 - 2x > 12x^2 +9x -8x -6\)
⇒ \(12x^2 - 2x > 12x^2 + x - 6\)
⇒ \(-2x-x>12x^2 -6-12x^2\)
⇒ \(- 3x > -6 \)
⇒ \(x > 2\)
S = {x / x > 2}
23 tháng 7 2021
Bài 1:
a) Ta có: \(2\left(3-4x\right)=10-\left(2x-5\right)\)
\(\Leftrightarrow6-8x-10+2x-5=0\)
\(\Leftrightarrow-6x+11=0\)
\(\Leftrightarrow-6x=-11\)
hay \(x=\dfrac{11}{6}\)
b) Ta có: \(3\left(2-4x\right)=11-\left(3x-1\right)\)
\(\Leftrightarrow6-12x-11+3x-1=0\)
\(\Leftrightarrow-9x-6=0\)
\(\Leftrightarrow-9x=6\)
hay \(x=-\dfrac{2}{3}\)
26 tháng 7 2017
\(3x-1\le23\)
\(\Leftrightarrow3x-1+1\le23+1\)
\(\Leftrightarrow3x\le24\)
\(\Leftrightarrow x\le8\)
26 tháng 7 2017
a,<=>3x<=24
<=>x<=8
Vậy ....
b, <=>4x-8>=9x-3-2x-1
<=>4x-9x+2x>=8-3-1
<=>-3x>=4
<=>x>=-4/3 Vậy ....
VP
7 tháng 5 2018
1) \(|3-5x|>=4\)
\(< =>\orbr{\begin{cases}3-5x>=4\\3-5x>=-4\end{cases}}\)
\(< =>\orbr{\begin{cases}-5x=1\\-5x=-7\end{cases}}\)
\(< =>\orbr{\begin{cases}x=\frac{-1}{5}\\x=\frac{7}{5}\end{cases}}\)
\(vay:x_1=\frac{-1}{5};x_2=\frac{7}{5}\)
CÂU 2 , 3 ,4 THÌ TƯƠNG TỰ ( CHIA THÀNH HAI TRƯỜNG HỢP RỒI GIẢI)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 4 2020
a/ \(\Leftrightarrow x^2-6x+9< 0\)
\(\Leftrightarrow\left(x-3\right)^2< 0\)
BPT vô nghiệm
b/ \(\Leftrightarrow12x^2-3x+1>0\)
\(\Leftrightarrow12\left(x-\frac{1}{8}\right)^2+\frac{13}{16}>0\) (luôn đúng)
Vậy tập nghiệm của BPT là \(D=R\)
c/ \(\Leftrightarrow2\left(x-4\right)\left(x-1\right)\left(x-3\right)>0\)
\(\Rightarrow\left[{}\begin{matrix}1< x< 3\\x>4\end{matrix}\right.\)
DP
9 tháng 7 2017
a, \(1-\frac{2x-1}{9}=3-\frac{3x-3}{12}\)
\(\Leftrightarrow\frac{108-12\cdot\left(2x-1\right)}{108}=\frac{108\cdot3-9\cdot\left(3x-3\right)}{108}\)
\(\Rightarrow108-12\cdot\left(x-1\right)=108\cdot3-9\cdot\left(3x-3\right)\)
\(\Leftrightarrow108-24x+12=324-27x+27\)
\(\Leftrightarrow3x=231\)
\(\Rightarrow x=77\)
c,\(\frac{3}{4x-20}+\frac{15}{50-2x^2}+\frac{7}{6x+30}=0\)
\(\Rightarrow3\cdot\left(50-2x^2\right)\cdot\left(6x+30\right)+15\cdot\left(4x-20\right)\cdot\left(6x+30\right)+7\cdot\left(4x-20\right)\cdot\left(50-2x^2\right)=0\)
\(\Leftrightarrow900x+4500-36x^3-180x^2+360x^2+1800x-1800x-9000+1400x-56x^3-7000+280x^2=0\)
\(\Leftrightarrow-92x^3+460x^2+2300x-11500=0\)
\(\Leftrightarrow92x^3-460x^2-2300x+11500=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=-5\\x=5\end{cases}}\)
28 tháng 5 2018
a) Thay x = 3 vào bất phương trình ta được: 2.3 + 3 < 9 <=> 9 < 9 (khẳng định sai)
Vậy x = 3 không là nghiệm của bất phương trình2x + 3 < 9
b) Thay x = 3 vào bất phương trình ta có: -4.3 > 2.3 + 5 => -12 > 11 (khẳng định sai)
Vậy x = 3 không là nghiệm của bất phương trình -4x > 2x + 5
c) Thay x = 3 vào bất phương trình ta có: 5 - 3 > 3.3 -12 => 2 > -3 (khẳng định đúng)
Vậy x = 3 là nghiệm của bất phương trình 5 - x > 3x - 12
C
1
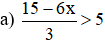
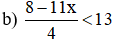
2x(6x – 1) > (3x – 2)(4x + 3)
⇔ 12x2 – 2x > 12x2 – 8x + 9x – 6
⇔ 12x2 – 2x – 12x2 + 8x – 9x > -6 (Chuyển vế, đổi dấu)
⇔ -3x > -6
⇔ x < 2 (Chia cả hai vế cho -3 < 0, BPT đổi chiều)
Vậy bất phương trình có nghiệm x < 2.