tìm giá trị lớn nhất của biểu thức:
H= -53- 25x^2+ 70x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
0
NH
2
15 tháng 11 2021
Mặt phẳng (P)(P) có VTPT −→nP=(1;2;−3)nP→=(1;2;−3); dd có VTCP →ud=(1;1;−1)ud→=(1;1;−1).
Gọi A=d∩(P)A=d∩(P), tọa độ điểm AA thỏa mãn hệ ⎧⎨⎩x+21=y−21=z−1x+2y−3z+4=0⇒A(−3;1;1){x+21=y−21=z−1x+2y−3z+4=0⇒A(−3;1;1).
Do ΔΔ nằm trong (P)(P) và vuông góc với dd nên có VTCP −→uΔ=[−→nP,→ud]=(1;−2;−1)uΔ→=[nP→,ud→]=(1;−2;−1).
Khi đó đường thẳng ΔΔ được xác định là đi qua A(−3;1;1)A(−3;1;1) và có VTCP −→uΔ=[−→nP,→ud]=(1;−2;−1)uΔ→=[nP→,ud→]=(1;−2;−1) nên có phương trình Δ:x+31=y−1−2=z−1−1Δ:x+31=y−1−2=z−1−1.
BK
2
16 tháng 8 2021
Đề bài sai, biểu thức này chỉ có Min, không có Max.
16 tháng 8 2021
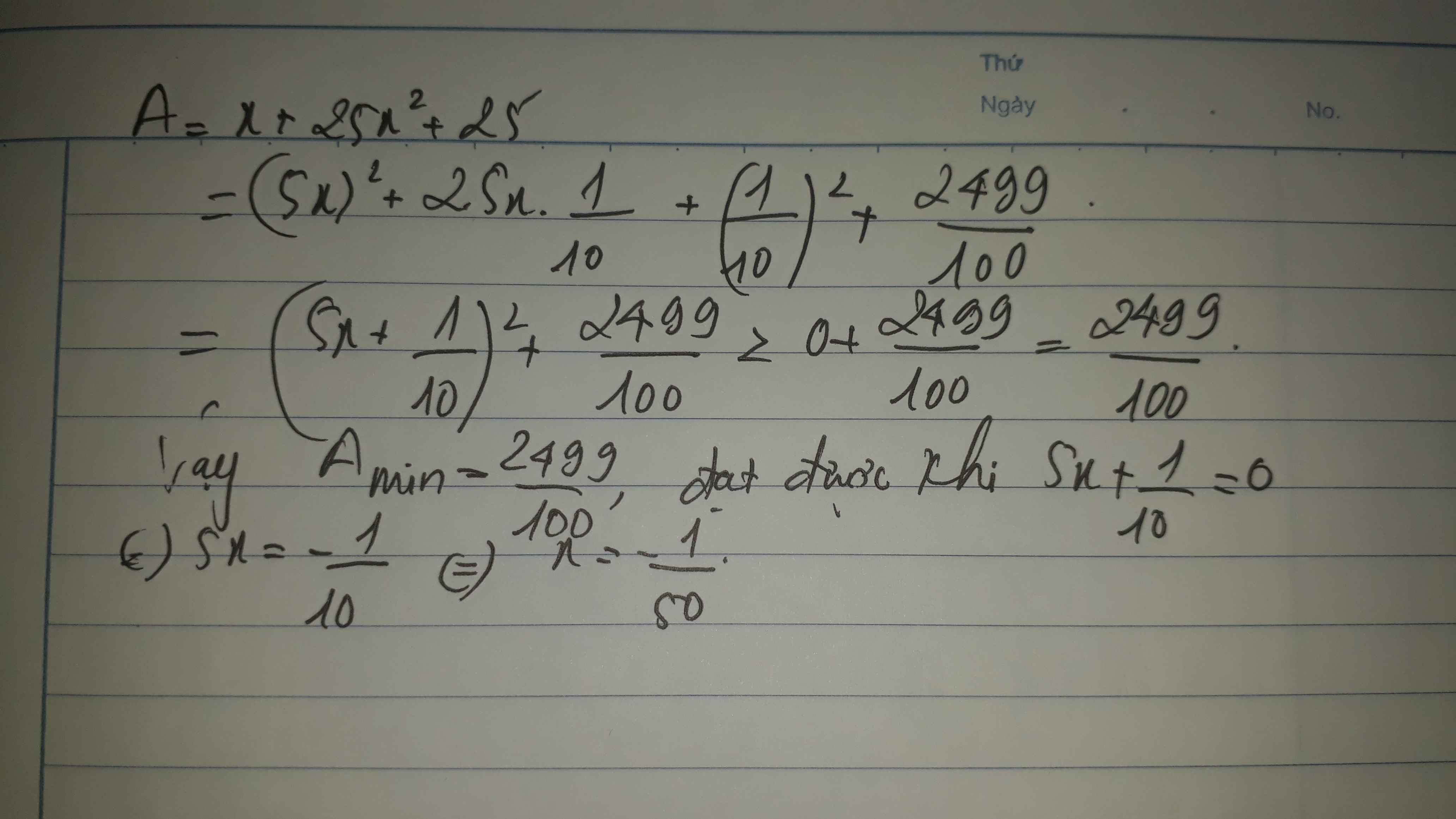
Ta có: \(25x^2+x+25\)
\(=\left(5x\right)^2+2\cdot5x\cdot\dfrac{1}{10}+\dfrac{1}{100}+\dfrac{2499}{100}\)
\(=\left(5x+\dfrac{1}{10}\right)^2+\dfrac{2499}{100}\ge\dfrac{2499}{100}\forall x\)
Dấu '=' xảy ra khi \(x=-\dfrac{1}{50}\)
18 tháng 9 2021
\(x=71\Leftrightarrow x-1=70\\ \Leftrightarrow A=x^5-\left(x-1\right)x^4-\left(x-1\right)x^3-\left(x-1\right)x^2-\left(x-1\right)x+34\\ A=x^5-x^5+x^4-x^4+x^3-x^3+x^2-x^2-x+x+34=34\)
18 tháng 9 2021
\(A=x^5-70x^4-70x^3-70x^2-70x+34\)
\(=x^4\left(x-71\right)+x^3\left(x-71\right)+x^2\left(x-71\right)+x^2\left(x-71\right)+x\left(x-71\right)+x+34\)
\(=x^4\left(71-71\right)+...+x\left(71-71\right)+71+34\)
\(=x^4.0+...+x.0+105=105\)
3 tháng 6 2019
\(C=\sqrt{25x^2-20x+4}+\sqrt{25x^2}\)
\(C=\sqrt{\left(5x-2\right)^2}+\sqrt{\left(5x\right)^2}\)
\(C=\left|5x-2\right|+\left|5x\right|=\left|2-5x\right|+\left|5x\right|\)
\(C\ge\left|2-5x+5x\right|=2\)
Dấu " = " xảy ra \(\Leftrightarrow\)( 2 - 5x ) . 5x \(\ge\)0
\(\Leftrightarrow\)\(\hept{\begin{cases}x\ge0\\2-5x\ge0\end{cases}}\)hoặc \(\hept{\begin{cases}x\le0\\2-5x\le0\end{cases}}\)
\(\Leftrightarrow\)\(0\le x\le\frac{2}{5}\)
Vậy GTNN của C là 2 \(\Leftrightarrow\)\(0\le x\le\frac{2}{5}\)
3 tháng 6 2019
\(C=\sqrt{25x^2-20x+4}+\sqrt{25x^2}\)
\(C=\sqrt{\left(5x-2\right)^2}+\sqrt{\left(5x\right)^2}\)
\(C=\left|5x-2\right|+\left|5x\right|\)
\(C=\left|2-5x\right|+\left|5x\right|\ge\left|2-5x+5x\right|=2\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}2-5x\ge0\\5x\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}x\le\frac{2}{5}\\x\ge0\end{cases}\Leftrightarrow0\le}x\le\frac{2}{5}}\)
NH
2
T
3 tháng 10 2019
\(B=25x^2+3y^2-10y+11\)
\(=25x^2+3\left(y^2-\frac{10}{3}y+\frac{11}{3}\right)\)
\(=25x^2+3\left(y^2-2.y.\frac{5}{3}+\frac{25}{9}+\frac{8}{9}\right)\)
\(=25x^2+3\left(y-\frac{5}{3}\right)^2+\frac{8}{3}\ge\frac{8}{3}\)
Đẳng thức xảy ra khi x = 0; y = 5/3
Vậy...
21 tháng 10 2016
A=...
dăt 5x=y viet cho gon
x=y/5
-A=y^2-y/5+3
=(y-1/10)^2+3-1/100
A=-(y-1/10)^2-299/100
GTLN=-299/100 khi y=1/10
\(H=-\left(25x^2-5\cdot2\cdot7x+49\right)-4\\ H=-\left(5x-7\right)^2-4\le-4\\ H_{max}=-4\Leftrightarrow x=\dfrac{7}{5}\)
\(=-\left(25x^2-70x+53\right)\)
\(=-\left(25x^2-2\cdot5x\cdot7+49+4\right)\)
\(=-\left(5x-7\right)^2-4\le-4\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{7}{5}\)