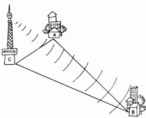
Ba thành phố A, B, C là ba đỉnh của một tam giác; biết rằng: AC = 30km, AB = 90km (h.20).
Nếu đặt ở C máy phát sóng truyền thanh có bán kính hoạt động bằng 60km thì thành phố B có nhận được tín hiệu không? Vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 6 2017
Để biết thành phố B có nhận được tín hiệu không thì phải tính được khoảng cách giữa hai thành phố B và C.
Sử dụng bất đẳng thức của tam giác và hệ quả vào ΔABC, ta có:
AB - AC < BC < AB + AC (1)
Thay các giá trị AB = 70km, AC = 30km vào (1), ta có:
70 - 30 < BC < 70 + 30 ⇔ 40 < BC < 100
Vì BC > 40 nên máy phát sóng để ở C có bán kính hoạt động bằng 40km thì B không nhận được tín hiệu.
CM
5 tháng 1 2020
Trong tam giác ABC có: BC < AC + AB (bất đẳng thức tam giác).
nên BC < 30 + 90 =120km
Nếu đặt tại C máy phát sóng truyền thanh có bán kính hoạt động bằng 120km thì thành phố B nhận được tín hiệu.
CM
2 tháng 9 2019
Để biết thành phố B có nhận được tín hiệu không thì phải tính được khoảng cách giữa hai thành phố B và C.
Sử dụng bất đẳng thức của tam giác và hệ quả vào ΔABC, ta có:
AB - AC < BC < AB + AC (1)
Thay các giá trị AB = 70km, AC = 30km vào (1), ta có:
70 - 30 < BC < 70 + 30 ⇔ 40 < BC < 100
Vì BC < 100 nên máy phát sóng để ở C có bán kính hoạt động bằng 100km thì B nhận được tín hiệu.
13 tháng 3 2018
a , ta có BC> AC+AB= 90+30=120 (Km)
vì sóng truyền thanh có bán kính là 60 km -> thành phố B không nhận được tín hiệu
b,
ta có BC> AC+AB= 90+30=120 (Km)
vì sóng truyền thanh có bán kính là 120 km -> thành phố B không nhận được tín hiệu
29 tháng 3 2018
Theo bất đẳng thức tam giác ta có:
\(\left|AC-AB\right|< BC< AC+AB\)
\(\left|30-70\right|< BC< 30+70\)
\(40< BC< 100\)
a) Máy phát sóng có bán kính 40km thì TP B ko nhận đc tín hiệu vì \(BC>\text{40}\)
b) Máy phát sóng có bán kính 100km thì TP B nhận đc tín hiệu vì \(BC< 100\)
31 tháng 5 2020
Để giải quyết câu hỏi của bài toán ta cần xét khoảng cách BC.
Trong ∆ABC theo bất đẳng thức của tam giác và hệ quả ta có: \(AB-AC< BC< AB+AC\)
Thay giá trị: AB = 70km, AC = 30km
\(\Rightarrow70-30< BC< 70+30\Rightarrow40< BC< 100\)
a) Nếu máy phát sóng để ở C có bán kính hoạt động bằng 40km thì ở B không nhận được tín hiệu vì BC > 40.
b) Nếu máy phát sóng để ở C có bán kính hoạt động bằng 100km thì ở B nhận được tín hiệu vì BC < 100.
CM
15 tháng 9 2017
Phương pháp:
Xác suất của biến cố A được tính bởi công thức: P A = n A n Ω
Cách giải:
Số cách chọn 3 đỉnh bất kì của đa giác là: n Ω = C 48 3
Gọi O là tâm đường tròn ngoại tiếp đa giác đều.
Gọi biến cố A: “Chọn 3 đỉnh bất kì của đa giác để được một tam giác nhọn”.
Lấy điểm A thuộc đường tròn (O), kẻ đường kính AA’ => A’ cũng thuộc đường tròn (O).
Khi đó AA’ chia đường tròn (O) thành hai nửa, mỗi nửa có 23 đỉnh.
Chọn 2 đỉnh B, C cùng thuộc 1 nửa đường tròn có C 23 2 c á c h c h ọ n ⇒ có C 23 2 tam giác ABC là tam giác tù.
Tương tự như vậy đối với nửa còn lại nên ta có 2 C 23 2 tam giác tù được tạo thành.
Đa giác đều có 48 đỉnh nên có 24 đường chéo => có 24.2. C 23 2 tam giác tù.
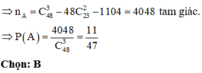
Ứng với mỗi đường kính ta có 23.2 tam giác vuông. Vậy số tam giác vuông là: 23.2.24 = 1104 tam giác.
Theo đề bài AC = 30km, AB = 90km ⇒ AC < AB.
Trong ∆ABC có: CB > AB – AC (hệ quả bất đẳng thức tam giác)
⇒ CB > 90 – 30 = 60km
Nếu đặt tại C máy phát sóng truyền thanh có bán kính hoạt động bằng 60km thì thành phố B không nhận được tín hiệu.