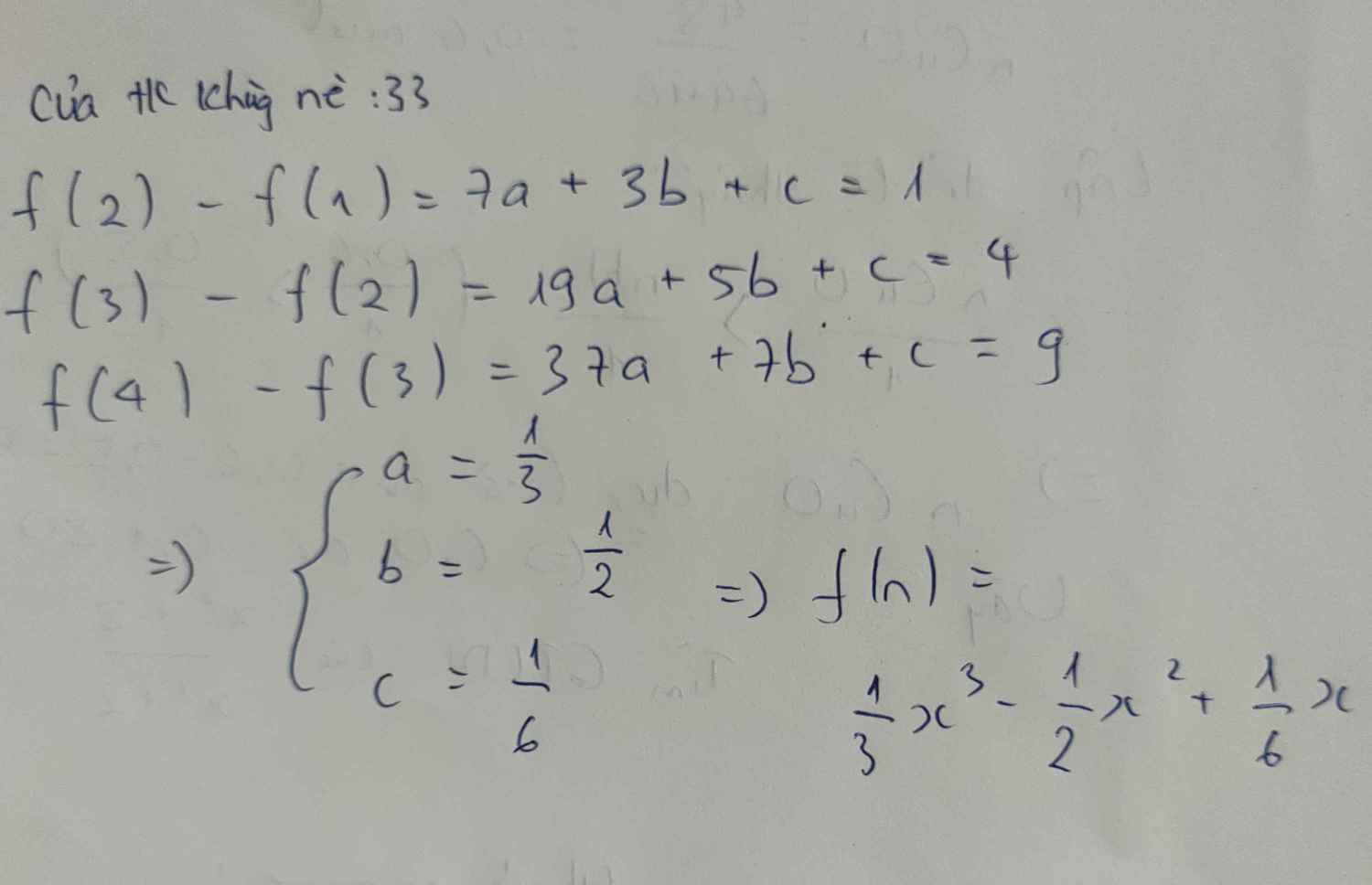Cho dãy số ( u n ) thoả mãn điều kiện: Với mọi n ∈ N ∗ thì 0 < u n

PT

Pham Trong Bach

5 tháng 3 2017

Cho dãy số ( u n ) thoả mãn điều kiện: Với mọi n ∈ N ∗ thì 0 < u n < 1 v à u n + 1 < 1 - ...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 11

1

CM

Cao Minh Tâm

5 tháng 3 2017

Đúng(0)

SG

Sách Giáo Khoa

10 tháng 4 2017

Cho dãy số \(\left(u_n\right)\) thỏa mãn điều kiện : Với mọi \(n\in N^{\circledast}\) thì

\(0< u_n< 1\) và \(u_{n+1}< 1-\dfrac{1}{4u_n}\)

Chứng minh dãy số đã cho là dãy giảm

#Hỏi cộng đồng OLM #Toán lớp 11

1

NT

Nguyen Thuy Hoa

19 tháng 5 2017

Dãy số - cấp số cộng và cấp số nhân

Đúng(1)

NL

Nguyễn Lan Phương

10 tháng 1 2017

cho dãy un biết u1=1/4 và u(n+1)=u(n)^2+u(n)/2 (n=1,2,...)

a,CMR:0<u(n)<=1/4

b,CMR: u(n+1)/u(n)<=3/4

c,tính lim u(n)

Mọi người giúp em với ạ! em cảm ơn!

#Hỏi cộng đồng OLM #Toán lớp 11

0

PH

Phú Hoàng Minh

24 tháng 1 2016 - olm

Bài 1: Chọn đáp án đúng:

Số nguyên n mà (n + 1)x(n + 3) < 0 là:

a) -5 b) -4 c) -3 d) -2

Bài 2: Tìm số nguyên n thõa mãn từng điều kiện sau:

(|n| + 2) x (n²-1) = 0

#Hỏi cộng đồng OLM #Toán lớp 6

1

VT

Vongola Tsuna

24 tháng 1 2016

câu 1: D ) -2

câu 2: chịu

Đúng(0)

LT

Lê Thị Ngọc Lan

24 tháng 8 2021 - olm

Cho số hữu tỷ :A = \(\frac{n-20}{30}\) với n là 1 số nguyên.

a) Tìm điều kiện của n để A > 0

b) Tìm điều kiện của n để 1 < A < 2

c) Có bao nhiêu số nguyên n thỏa mãn \(\frac{1}{2}\) < A < 1

#Hỏi cộng đồng OLM #Toán lớp 7

1

ND

Nguyễn Đức Chung

24 tháng 8 2021

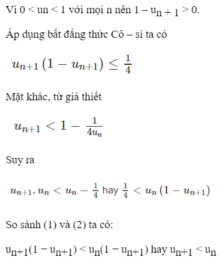
a) Để A>0 thì \(\frac{n-20}{30}>0\) mà 30>0 nên n-20>0 hay n>20

b) \(1< A< 2\Leftrightarrow\frac{30}{30}< \frac{n-20}{30}< \frac{60}{30}\)

\(\Rightarrow30< n-20< 60\)

\(\Rightarrow50< n< 80\)( Cộng 3 vế với 20 )

c) Tương tự câu b :

\(\frac{15}{30}< \frac{n-20}{30}< \frac{30}{30}\Leftrightarrow15< n-20< 30\)

\(\Rightarrow35< n< 50\)

\(n\in\left\{36;37;...;49\right\}\)

Nên n có \(49-36+1\)số hạng hay n có 14 số hạng

Đúng(0)

HB

Hán Bình Nguyên

3 tháng 6 2021

Cho dãy xác định \(\left\{{}\begin{matrix}u\left(1\right)=\dfrac{1}{2}\\u\left(n+1\right)=\dfrac{u\left(n\right)}{n+1}\end{matrix}\right.\)

a, CM : với mọi n thì 0<u(n) và \(\dfrac{u\left(n\right)}{n+1}\)\(\le\dfrac{1}{2}\)

b, Từ đó suy ra limu(n)=0

#Hỏi cộng đồng OLM #Toán lớp 11

0

HB

Hán Bình Nguyên

3 tháng 6 2021

Cho dãy xác định \(\left\{{}\begin{matrix}u\left(1\right)=\dfrac{1}{4}\\u\left(n+1\right)=\left(u\left(n\right)\right)^2+\dfrac{u\left(n\right)}{2}\end{matrix}\right.\)

CM với mọi n thì 0<u(n)<\(\dfrac{1}{4}\) và\(\dfrac{u\left(n+1\right)}{u\left(n\right)}\le\dfrac{3}{4}\)

Từ đó suy ra limu(n)=o

#Hỏi cộng đồng OLM #Toán lớp 11

0

CC

Chích cuồq Khiêm thương Khiêm yêu K...

7 tháng 4 2016 - olm

Bài 1: Tìm số nguyên n sao cho:n+1 chia hết cho n²+5

Bài 2:Chứng minh rằng với mọi số tự nhiên n khác 0 thì:3ⁿ⁺³+2.3ⁿ+2ⁿ⁺⁵-3.2ⁿ chia hết cho 29

Bài 3: cho a,b,c thoả mãn: a+b+c=0. CMR:ab+bc+ca<=0

#Hỏi cộng đồng OLM #Toán lớp 7

0

TT

Trần Tuấn Hoàng

9 tháng 2 2022

Tìm các hằng số a, b, c sao cho đa thức f(x) =ax² + bx + c thoả mãn điều kiện

f(n+1) – f(n) = n² với mọi n = 1, 2, …

#Hỏi cộng đồng OLM #Toán lớp 9

2

AM

Ami Mizuno

9 tháng 2 2022

Không biết đề có vấn đề không nữa, tại vì không có cách nào để rút được c ra hết do f(n+1)-f(n) kiểu gì c cũng bị khử. Tuy nhiên nếu xét trường hợp với mọi c thì thay n=3 trở lên giải ngược lại không có nghiệm c nào thỏa mãn hết hehe nên là mình nghĩ đề sẽ kiểu "với n=1 hoặc n=2" . Theo mình nghĩ là vậy...

Giả sử n=1 ta có:

\(f\left(1+1\right)-f\left(1\right)=1\Leftrightarrow f\left(2\right)-f\left(1\right)=1\Leftrightarrow4a+2b+c-a-b-c=1\Leftrightarrow3a+b=1\) (1)

Giả sử n=2 ta có:

\(f\left(2+1\right)-f\left(2\right)=4\Leftrightarrow f\left(3\right)-f\left(2\right)=4\Leftrightarrow9a+3b+c-4a-2b-c=4\Leftrightarrow5a+b=4\) (2)

Từ (1) và (2) ta có: \(\left\{{}\begin{matrix}3a+b=1\\5a+b=4\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=\dfrac{3}{2}\\b=-\dfrac{7}{2}\end{matrix}\right.\)

\(\Rightarrow f\left(x\right)=\dfrac{3}{2}x^2-\dfrac{7}{2}x+c\) (với c là hằng số bất kì)

Đúng(0)

DT

Đỗ Tuệ Lâm

9 tháng 2 2022

undefined

Đúng(0)

PL

Phạm la

29 tháng 4 2017

câu1.nếu hai số x và y thỏa mãn điều kiện 0<x<y và 2x^2 + 2y^2 = 5xy thì biểu thức P = x-y/x+y có giả trị là ?

câu 2.một số tiền x được gửi tiết kiệm với lãi suất 7,5% trong một năm . sau một năm thì số tiền x được nhân với số bao nhiêu ?

câu 3 . cho các số dương a , b thỏa mãn a^3+b^3 = a-b . chứng minh rằng a^2+ab+b^2<1

#Hỏi cộng đồng OLM #Toán lớp 8

1

PA

Phương An

29 tháng 4 2017

Câu 1:

2x² + 2y² = 5xy

<=> 2(x² + y²) = 5xy

<=> x² + y² = \(\dfrac{5xy}{2}\)

P = \(\dfrac{x-y}{x+y}\)

=> P² = \(\dfrac{\left(x-y\right)^2}{\left(x+y\right)^2}=\dfrac{x^2+y^2-2xy}{x^2+y^2+2xy}\left(1\right)\)

Thay x² + y² = \(\dfrac{5xy}{2}\) vào (1), ta có:

P² = \(\dfrac{\dfrac{5xy}{2}-2xy}{\dfrac{5xy}{2}+2xy}=\dfrac{0,5xy}{4,5xy}=\dfrac{1}{9}\)

=> P = \(\sqrt{\dfrac{1}{9}}=\dfrac{1}{3}\left(0< x< y\right)\)

Câu 3: Câu hỏi của Hoàng Mai Anh - Toán lớp 8 | Học trực tuyến

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP