Tìm a ∈ (0; 2 π ) để hàm số sau đồng biến trên khoảng (1; + ∞ ).
y = 1 3 x 3 - 1 2 (1 + cosa) x 2 + 2x cosa + 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 8 2021
1: Để A>0 thì x-1<0
hay x<1
Kết hợp ĐKXĐ, ta được: \(0\le x< 1\)
29 tháng 8 2021
1) Để A > 0 thì:
\(x-1< 0\Leftrightarrow x< 1\)
\(\Rightarrow0\le x< 1\) và \(x\ne1\)
2) \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=1+\dfrac{2}{\sqrt{x}-1}\)
Để A<1 thì \(\dfrac{2}{\sqrt{x}-1}< 0\)
\(\Rightarrow\sqrt{x}-1< 0\Leftrightarrow\sqrt{x}< 1\)
Mà x\(\ge0,x\ne1\)
\(\Rightarrow0\le x< 1\)
MY
3
17 tháng 3 2018
\(b)\) Để \(A>0\) thì :
Trường hợp 1 :
\(\hept{\begin{cases}5x+2>0\\8x-1>0\end{cases}\Leftrightarrow\hept{\begin{cases}5x>-2\\8x>1\end{cases}\Leftrightarrow}\hept{\begin{cases}x>\frac{-2}{5}\\x>\frac{1}{8}\end{cases}}}\)
\(\Rightarrow\)\(x>\frac{1}{8}\)
Trường hợp 2 :
\(\hept{\begin{cases}5x+2< 0\\8x-1< 0\end{cases}\Leftrightarrow\hept{\begin{cases}5x< -2\\8x< 1\end{cases}\Leftrightarrow}\hept{\begin{cases}x< \frac{-2}{5}\\x< \frac{1}{8}\end{cases}}}\)
\(\Rightarrow\)\(x< \frac{-2}{5}\)
Vậy để \(A>0\) thì \(x>\frac{1}{8}\) hoặc \(x< \frac{-2}{5}\)
Chúc bạn học tốt ~
17 tháng 3 2018
\(a)\) Để \(A=0\) thì :
\(5x+2=0\)
\(\Rightarrow\)\(5x=-2\)
\(\Rightarrow\)\(x=\frac{-2}{5}\)
Vậy để \(A=0\) thì \(x=\frac{-2}{5}\)
HB
Cho ps A = 4x-3/2x+1
a, Tìm x để A > 0
b Tìm x để A < 0
c , tìm x để A = 0
đ tìm x thuộc Z để A thuộc Z
1
13 tháng 12 2015
\(A=\frac{4x-3}{2x+1}=\frac{4x+2-5}{2x+1}=2-\frac{5}{2x+1}\)
a) A>0 => \(\frac{5}{2x+1}<2\Leftrightarrow2x+1>\frac{5}{2}\Leftrightarrow2x>\frac{3}{2}\Leftrightarrow x>\frac{3}{4}\)
b)A<0 => x <3/4 ; x khác -1/2
c)A =0 khi x = 3/4
d) A thuộc Z khi 2x+1 thuộc U(5) ={1;5;-1;-5}
2x+1 =1 => x =0
2x+1=-1 => x = -1
2x+1 =5 => x =2
2x+1 = -5 => x =-3
AN
0
GN
1
LM
5 tháng 9 2016
a, Để A = 0 thì x = 0 hoặc \(\left(x-\frac{1}{2}\right)\)= 0 => x = 0 hoặc x = 0,5
b, Để A > 0 thì x > 0 và \(\left(x-\frac{1}{2}\right)\)> 0 hoặc x < 0 và \(\left(x-\frac{1}{2}\right)\)< 0
=> x > 0 và x > 0,5 hoặc x < 0 và x < 0,5
c,a, Để A < 0 thì x > 0 và \(\left(x-\frac{1}{2}\right)\)< 0 hoặc x < 0 và \(\left(x-\frac{1}{2}\right)\)> 0 mà x > \(\left(x-\frac{1}{2}\right)\) => x > 0 và x < 0,5
MC
0
10 tháng 9 2021
a) \(A=x\left(x-\dfrac{4}{9}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{4}{9}\end{matrix}\right.\)
b) \(A=x\left(x-\dfrac{4}{9}\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x< 0\\x-\dfrac{4}{9}< 0\end{matrix}\right.\\\left\{{}\begin{matrix}x>0\\x-\dfrac{4}{9}>0\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x< 0\\x>\dfrac{4}{9}\end{matrix}\right.\)
c) \(A=x\left(x-\dfrac{4}{9}\right)< 0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>0\\x-\dfrac{4}{9}< 0\end{matrix}\right.\)( do \(x>x-\dfrac{4}{9}\))
\(\Leftrightarrow\dfrac{4}{9}>x>0\)
LT
10 tháng 9 2021
a) A=x.(x-4/9)=0
<=>X=0 và X=4/9
b). A=x.(x-4/9)>0
<=>X>0 và X>4/9
c). A=x.(x-4/9)<0
<=>X<0 và X<4/9
8 tháng 8 2019
Ta có:
\(0,b\times0,a\times0,b=\overline{0,bbb}\)
nhân cả hai vế với 1000 .
\(0,b\times0,a\times0,b\times1000=\overline{0,bbb}\times1000\)
\(\left(0,b\times10\right)\times\left(0,a\times10\right)\times\left(0,b\times10\right)=\overline{bbb}\)
\(b\times a\times b=b\times111\)
\(b\times a\times b-b\times111=0\)
\(b\times\left(a\times b-111\right)=0\)
ta có: a, b là các số tự nhiên, \(0\le a,b\le9\)=> \(a\times b\le81\)<111
nên suy ra b=0
Vậy b =0 và a bất kì
( Mình nghĩ là bạn sai đề rồi )
11 tháng 7 2018
ĐKXĐ: \(x\ne-5;0\)
\(A=\frac{x^2+2x}{2x+10}+\frac{x-5}{x}+\frac{50-5x}{2x.\left(x+5\right)}\)
\(=\frac{\left(x^2+2x\right).x}{2x.\left(x+5\right)}+\frac{2.\left(x+5\right).\left(x-5\right)}{2x.\left(x+5\right)}+\frac{50-5x}{2x\left(x+5\right)}\)
\(=\frac{x^3+2x^2}{2x\left(x+5\right)}+\frac{2.\left(x^2-25\right)}{2x\left(x+5\right)}+\frac{50-5x}{2x\left(x+5\right)}=\frac{x^3+2x^2+2x^2-50+50-5x}{2x\left(x+5\right)}\)
\(=\frac{x^3+4x^2-5x}{2x\left(x+5\right)}=\frac{x\left(x^2+4x-5\right)}{2x\left(x+5\right)}=\frac{x\left(x+5\right)\left(x-1\right)}{2x\left(x+5\right)}=\frac{x-1}{2}\)
b. \(A=0\Leftrightarrow\frac{x-1}{2}=0\Rightarrow x-1=0\Leftrightarrow x=1\)
\(A=\frac{1}{4}\Leftrightarrow\frac{x-1}{2}=\frac{1}{4}\Leftrightarrow4x-4=2\Leftrightarrow4x-6=0\Leftrightarrow x=\frac{3}{2}\)
c. Với x=0 thì \(A=\frac{0-1}{2}=-\frac{1}{2}\)
Với x=2 thì: \(A=\frac{2-1}{2}=\frac{1}{2}\)
d. \(A>0\Leftrightarrow\frac{x-1}{2}>0\Rightarrow\left(x-1\right).2>0\Rightarrow x-1>0\Leftrightarrow x>1\)
\(A< 0\Leftrightarrow\frac{x-1}{2}< 0\Leftrightarrow\left(x-1\right).2< 0\Leftrightarrow x-1< 0\Leftrightarrow x< 1;x\ne-5,0\)
e. \(A=\frac{x-1}{2}\inℤ\Rightarrow x-1\in Z\Rightarrow x\inℤ\)
Và \(\left(x-1\right)⋮2\Rightarrow x:2dư1\)
Vậy \(A\in Z\Leftrightarrow x\inℤ\)và x chia 2 dư 1
Tập xác định: D = R; y′ = x 2 − (1 + 2cosa)x + 2cosa
y′= 0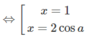
Vì y’ < 0 ở ngoài khoảng nghiệm nên để hàm số đồng biến với mọi x > 1 thì 2cosa ≤ 1
(vì a ∈ (0; 2 π ).