Tính số các số hạng của cấp số cộng (an), nếu a 2 + a 4 + . . . + a 2 n = 126 a 2 + a 2 n = 42
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


#include <bits/stdc++.h>
using namespace std;
double n,a,d;
int main()
{
cin>>n>>a>>d;
cout<<fixed<<setprecision(2)<<n*(a+d)/2;
return 0;
}

a)
n = 20 tức n chẵn.
Khi n chẵn: \(A=-4.\dfrac{n}{2}=-4.\dfrac{20}{2}=-40\)
b)
Khi n chẵn:
\(A=-4.\dfrac{n}{2}=-2n\)
Khi n lẽ:
\(A=1+\dfrac{4\left(n-1\right)}{2}=1+2\left(n-1\right)=1+2n-2=2n-1\)

a) Số hạng thứ 20 (n=20) là
\(\left(20-1\right).4=76\)
\(A=1-5+9-13+17-21+...+76\)
\(A=\left(-4\right)+\left(-4\right)+\left(-4\right)+...+\left(-4\right)\)
\(A=\left(-4\right).38=-152\)
b) Số hạng thứ n là:
\(\left(n-1\right).4\)
\(\)\(A=1-5+9-13+17-21+...+\left(n-1\right).4\)
\(A=\left(-4\right)+\left(-4\right)+\left(-4\right)+...+\left(-4\right)\) ((n-1).2 số -4)
\(A=\left(-4\right).\left(n-1\right).2=-8\left(n-1\right)\)

Gọi công bội của cấp số nhân là q => b=a.q; c=a.q^2
Gọi công sai của cấp số cộng là d => b=a+2d; c=a+8d
Ta có: a.q=a+2d => \(q=\dfrac{a+2d}{a}=1+2\dfrac{d}{a}\)
\(a.q^2=a+8d\Rightarrow q^2=\dfrac{a+8d}{a}=1+8\dfrac{d}{a}\)
Suy ra \(\left(1+2\dfrac{d}{a}\right)^2=1+8\dfrac{d}{a}\Rightarrow\dfrac{d}{a}=1\left(d\ne0\right)\)
=> b=a+2a=3a; c=a+8a=9a
Theo bài ra a+b+c=26 => a+3a+9a=13a=26 => a=2; b=6; c=18
Vậy ba số cần tìm là a=2; b=6; c=18

Chọn C
Gọi ba số đó lần lượt là x,y,z
Do ba số là các số hạng thứ 2, thứ 9 và thứ 44 của một cấp số cộng nên ta có liên hệ: y = x + 7 d , z = x + 42 (với d là công sai của cấp số cộng)
Theo giả thiết ta có: x + y + z = x + x + 7 d + x + 42 d = 3 x + 49 d = 217
Mặt khác do x,y,z là các số hạng liên tiếp của một cấp số nhân nên
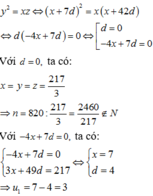
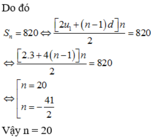

a) \({u_1} = 8;\;\;\;\;{u_2} = 13;\;\;\;\;\;{u_3} = 18;\;\;\;\;\;{u_4} = 23;\;\;\;\;\;{u_5} = 28\).
Ta có: \({u_n} - {u_{n - 1}} = 3 + 5n - \left[ {3 + 5\left( {n - 1} \right)} \right] = 5,\;\forall n \ge 2\).
Vậy dãy số \(\left( {{u_n}} \right)\) là cấp số cộng với \({u_1} = 8\) và công sai \(d = 5\).
Số hạng tổng quát: \({u_n} = 8 + 5\left( {n - 1} \right)\).
b) \({u_1} = 2;\;\;\;\;{u_2} = 8;\;\;\;\;{u_3} = 14;\;\;\;\;\;{u_4} = 20;\;\;\;\;\;{u_5} = 26\).
Ta có: \({u_n} - {u_{n - 1}} = 6n - 4 - \left[ {6\left( {n - 1} \right) - 4} \right] = 6,\;\forall n \ge 2\).
Vậy dãy số \(\left( {{u_n}} \right)\) là cấp số cộng với \({u_1} = 2\) và công sai \(d = 6\).
Số hạng tổng quát: \({u_n} = 2 + 6\left( {n - 1} \right)\).
c) \({u_1} = 2;\;\;\;\;{u_2} = 4;\;\;\;\;\;{u_3} = 7;\;\;\;\;\;\;{u_4} = 11;\;\;\;\;\;\;\;{u_5} = 16\)
Ta có: \({u_n} - {u_{n - 1}} = n,\;\) n biến động.
Suy ra đây không phải là cấp số cộng.
d) \({u_1} = 2;\;\;\;\;{u_2} = 5;\;\;\;\;\;\;{u_3} = 8;\;\;\;\;\;\;{u_4} = 11;\;\;\;\;\;\;\;{u_5} = 14\)
Ta có: \({u_n} - {u_{n - 1}} = 3\).
Vậy dãy số \(\left( {{u_n}} \right)\) là cấp số cộng với \({u_1} = 2\) và công sai \(d = 3\).
Số hạng tổng quát: \({u_n} = 2 + 3\left( {n - 1} \right),\;\forall n \ge 2\).
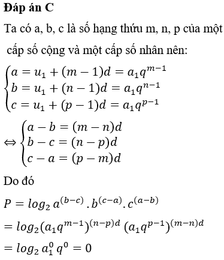
Đáp số: n = 6