Một con lắc đơn có sợi dây dài 1m và vật nặng có khối lượng 500g. Kéo vật lệch khỏi vị trí cân bằng sao cho cho dây làm với đường thẳng đứng một góc 60o rồi thả nhẹ. Lấy g = 10 ( m / s 2 )
a. Xác định cơ năng của con lắc đơn trong quá trình chuyển động
b. Tính vận tốc của con lắc khi nó đi qua vị trí mà dây làm với đường thẳng đứng góc 30 0 ; 45 0 và xác định lực căng của dây ở hai vị trí đó. Lấy g=10m/s2
c. Xác định vị trí để vật có v= 1,8 m/s
d. Ở vị trí vật có độ cao 0,18m vật có vận tốc bao nhieu
e. Xác định vận tốc tại vị trí 2 w t = w đ
f. Xác định vị trí để 2 w t = 3 w đ , tính vận tốc và lực căng khi đó


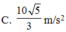
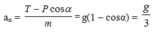

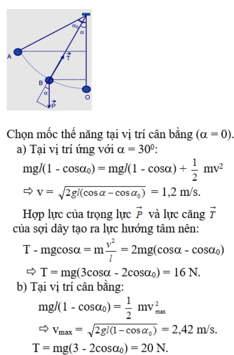
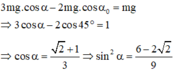
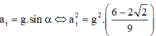
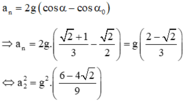
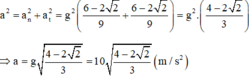
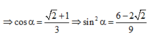
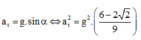
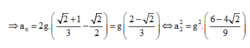
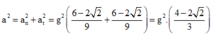
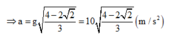
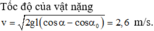
Chọn mốc thế năng ở vị trí cân bằng
a. Ta có cơ năng
W = m g z = m g l ( 1 − cos 60 0 ) = 0 , 5.10.1 ( 1 − 0 , 5 ) = 2 , 5 ( J )
b. Theo định luật bảo toàn cơ năng
W A = W B ⇒ m g z A = 1 2 m v B 2 + m g z B ⇒ v B = 2 g ( z A − z B ) ( 1 ) M à z A = H M = l − O M = l − l cos α 0 z B = l − l cos α
Thay vào ( 1 ) ta có
v B = 2 g l ( cos α − cos α 0 ) + K h i α = 30 0 ⇒ v B = 2 g l ( cos 30 0 − cos 60 0 ) ⇒ v B = 2.10.1 ( 3 2 − 1 2 ) ≈ 2 , 71 ( m / s )
+ K h i α = 45 0 ⇒ v B = 2 g l ( cos 45 0 − cos 60 0 ) ⇒ v B = 2.10.1 ( 2 2 − 1 2 ) ≈ 2 , 035 ( m / s )
Xét tai B theo định luật II Newton ta có: P → + T → = m a →
Chiếu theo phương của dây
T − P y = m a h t ⇒ T − P cos α = m v 2 l ⇒ T − m g cos α = 2 m g ( cos α − cos α 0 ) ⇒ T = m g ( 3 cos α − 2 cos α 0 )
Khi α = 30 0 ⇒ T = m g ( 3 cos 30 0 − 2 cos 60 0 )
⇒ T = 0 , 5.10 ( 3. 3 2 − 2. 1 2 ) = 7 , 99 ( N )
Khi α = 45 0 ⇒ T = m g ( 3 cos 45 0 − 2 cos 60 0 )
⇒ T = 0 , 5.10 ( 3. 2 2 − 2. 1 2 ) = 5 , 61 N
Lưu ý: Khi làm trắc nghiệm thì các em áp dụng luôn hai công thức
+ Vận tốc của vật tại vị trí bất kỳ: v B = 2 g l ( cos α − cos α 0 )
+ Lực căng của sợi dây: T = m g ( 3 cos α − 2 cos α 0 )
c. Gọi C là vị trí để vật có v= 1,8m/s
Áp dụng công thức v C = 2 g l ( cos α − cos α 0 )
1 , 8 = 2.10.1 ( cos α − cos 60 0 ) ⇒ cos α = 0 , 662 ⇒ α = 48 , 55 0
Vật có đọ cao
z C = l − l cos α = 1 − 1.0 , 662 = 0 , 338 ( m )
d. Gọi D là vị trí vật có độ cao 0,18m
Áp dụng công thức
z D = l − l cos α ⇒ 0 , 18 = 1 − 1. cos α ⇒ cos α = 0 , 82
Áp dụng công thức
v D = 2 g l ( cos α − cos α 0 ) = 2.10.1. ( 0 , 82 − 0 , 5 ) = 2 , 53 ( m / s )
e. Gọi E là vị trí mà 2 w t = w đ Theo định luật bảo toàn cơ năng W A = W E
W A = W d E + W t E = 3 2 W d E ⇒ 2 , 5 = 3 2 . 1 2 . m v E 2 ⇒ v E = 2 , 5.4 3. m = 10 3.0 , 5 = 2 , 581 ( m / s )
f. Gọi F là vị trí để 2 w t = 3 w đ
Theo định luật bảo toàn cơ năng W A = W F
W A = W d F + W t F = 5 3 W t F ⇒ 2 , 5 = 5 3 . m g z F ⇒ z F = 2 , 5.3 5. m . g = 0 , 3 ( m ) M à z F = l − l cos α F ⇒ 0 , 3 = 1 − 1. cos α F ⇒ cos α F = 0 , 7 ⇒ α F = 45 , 573 0
Mặt khác v F = 2 g l ( cos α F − cos 60 0 ) = 2.10.1 ( 0 , 7 − 0 , 5 ) = 2 ( m / s )
Xét tại F theo định luật II Newton P → + T → = m a →
Chiếu theo phương của dây
− P cos α F + T F = m v F 2 l ⇒ − 0 , 5.10.0 , 7 + T F = 0 , 5. 2 2 1 ⇒ T = 5 , 5 ( N )