Trong thí nghiệm ở hình 8.1, vận tốc truyền sóng là 0,5 m/s, cần rung có tần số 40Hz. Tính khoảng cách giữa hai điểm cực đại giao thoa cạnh nhau trên đoạn thẳng S1S2.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
5 tháng 11 2023
Ta có: v = 20 cm/s = 0,2 m/s
Bước sóng là: λ= \(\frac{v}{f} = \frac{{0,2}}{{40}}\)= 0,005 (m)
Do: khoảng cách giữa 2 cực đại giao thoa cạnh nhau trên đoạn S1S2 = khoảng cách giữa 2 cực tiểu giao thoa cạnh nhau trên đoạn S1S2 = \(\frac{\lambda }{2}\).
⇒ Khoảng cách giữa hai điểm cực đại giao thoa trên đoạn S1S2 là:
d= \(\frac{\lambda }{2}\) = \(\frac{{0,005}}{2}\)= 0,0025 (m)
VT
24 tháng 2 2019
Đáp án: C
HD Giải: λ = v f = 60 100
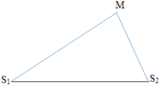
Điểm dao động với biên độ cực đại trên đoạn MS1 thỏa mãn:
<=> 
<=> 
có 6 cực đại trên MS1
VT
3 tháng 1 2019
Đáp án A
Bước sóng: λ = v.T = v/f = 80/40 = 2cm
=> Khoảng cách ngắn nhất giữa hai điểm cực đại giao thoa trên đoạn thẳng S 1 S 2 là λ/2 = 1cm
VT
6 tháng 4 2019
Đáp án A
Bước sóng: λ = v.T = v/f = 80/40 = 2cm
=> Khoảng cách ngắn nhất giữa hai điểm cực đại giao thoa trên đoạn thẳng S1S2 là λ/2 = 1cm
VT
22 tháng 1 2017
Trên đoạn thẳng nối hai nguồn khoảng cách giữa một cực đại và một cực tiểu liên tiếp là d=λ/4=1cm
Tốc độ truyền sóng v=λf=1(m/s)
Chọn đáp án A
Bước sóng dùng trong thí nghiệm là: λ = v/f = 0,5/ 40 = 0,0125m = 1,25cm
Khoảng cách giữa hai điểm cực đại giao thoa cạnh nhau trên đoạn thẳng S1S2 bằng nửa bước sóng.
Ta có: d = λ/2 = 1,25/2 = 0,625cm