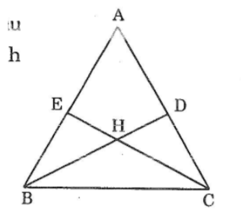
Trên hình bên có một số tam giác bằng nhau. Hãy quan sát rồi phát hiện các tam giác bằng nhau trong hình vẽ (không xét các tam giác mà các cạnh chưa được kẻ), sau đó kiểm tra lại bằng cách đo.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các tam giác = nhau là :
\(\Delta ABD\) và \(\Delta BDC\)
\(\Delta BEH\) và \(\Delta CDH\)
\(\Delta AEC\) và \(\Delta BEC\)
Tick minh ha

a) Chỉ có ABC là hình có 3 cạnh bằng nhau.
b) Các góc của tam giác ABC bằng nhau và đều bằng \(60^\circ \) .

+ ΔABD = ΔCBD (g.c.g) vì:
∠ABD = ∠CBD (gt)
BD chung
∠ADB = ∠BDC (= 90o)
+ Ta có: ∠FGI = ∠IHE ( giả thiết). Mà hai góc này ở vị trí so le trong nên: FG // HE
⇒ ∠GFI = ∠IEH ( hai góc so le trong).
*) Khi đó: ΔGIF = ΔHIE (g.c.g) vì:
∠GFI = ∠IEH ( chứng minh trên)
FI = IE ( giả thiết)
∠GIF = ∠EIH (hai góc đối đỉnh)

-Xét tam giác vuông BDA và tam giác vuông BDC có:
ABD = CBD
BD: cạnh chung
=> tam giác BDA = tam giác BDC
-Ta có: góc G = góc H
góc FIG = góc EIH
Mà F + G + FIG = E + H + EIH = 1800
=> góc F = góc E
Xét tam giác IFG và tam giác IEH có:
IF = IE (gt)
FIG = EIH (gt)
góc F = góc E (cmt)
=> tam giác IFG = tam giác IEH

a: Đúng
b: Sai. Hình chóp tứ giác đều có các cạnh bên bằng nhau và các cạnh đáy bằng nhau

a) Các mặt bên của mỗi hình a, b là các hình chữ nhật
Các mặt bên của mỗi hình c, d là hình tam giác
b) Hình c có cách cạnh bên bằng nhau và đáy là tam giác đều
c) Hình d có các cạnh bên bằng nhau và đáy là hình vuông
a:
1a,1b: Hình chữ nhật
1c,1d: Hình tam giác
b:
Cả bốn hình đều có các cạnh bên bằng nhau
1c,1a là hai hình là các đáy là tam giác đều
c: Hình 1b và hình 1d có đáy là hình vuông
Có ba cặp tam giác bằng nhau:
ΔABD=ΔACE
ΔBEC=ΔCDB
ΔBEH=ΔCDH