Khử mẫu của biểu thức lấy căn a b a b ; a b b a ; 1 b + 1 b 2 ; 9 a 2 36 b ; 3 x z 2 x y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
QA
0
24 tháng 8 2023
a: \(\sqrt{\dfrac{3}{20}}=\sqrt{\dfrac{15}{100}}=\dfrac{\sqrt{15}}{10}\)
b: \(\sqrt{\dfrac{5}{18}}=\sqrt{\dfrac{10}{36}}=\dfrac{\sqrt{10}}{6}\)
c: \(ab\sqrt{\dfrac{a}{b}}=ab\cdot\dfrac{\sqrt{a}}{\sqrt{b}}=a\sqrt{ab}\)
d: \(\dfrac{x}{y}\sqrt{\dfrac{y}{x}}=\dfrac{x}{y}\cdot\dfrac{\sqrt{y}}{\sqrt{x}}=\sqrt{\dfrac{x}{y}}=\dfrac{\sqrt{xy}}{y}\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 7 2021
\(=\sqrt{\dfrac{b+1}{b^2}}=\left[{}\begin{matrix}\dfrac{\sqrt{b+1}}{b}\left(b>0\right)\\-\dfrac{\sqrt{b+1}}{b}\left(-1\le b< 0\right)\end{matrix}\right.\)
HH
29 tháng 6 2018
Giải:
a) \(\dfrac{a}{b}\sqrt{\dfrac{b}{a}}\)
\(=\sqrt{\dfrac{b}{a}.\left(\dfrac{a}{b}\right)^2}\)
\(=\sqrt{\dfrac{b}{a}.\dfrac{a^2}{b^2}}\)
\(=\sqrt{\dfrac{a^2.b}{ab^2}}\)
\(=\sqrt{\dfrac{a}{b}}\)
Vậy ...
b) \(3xy\sqrt{\dfrac{2}{xy}}\)
\(=\sqrt{\dfrac{2.\left(3xy\right)^2}{xy}}\)
\(=\sqrt{\dfrac{2.9x^2y^2}{xy}}\)
\(=\sqrt{18xy}\)
Vậy ...
31 tháng 3 2017
có nghĩa khi
và
Nếuthì
Nếuthì
- Tương tự như vậy ta có:
Nếuthì
Nếu - Ta có:
Điều kiện để căn thức có nghĩa làhay
Do đó:
Nếu b>0 thì
Nếuthì
- Điều kiện để
có nghĩa là
hay
Cách 1.
=
Cách 2. Biến mẫu thành một bình phương rồi áp dụng quy tắc khai phương một thương: - Điều kiện để
có nghĩa là
hay xy>0.
Do đó
PT
1
CM
3 tháng 9 2017
(Ghi nhớ: Khử căn ở mẫu tức là nhân cả tử và mẫu với thừa số có chứa căn.)
PT
1
CM
13 tháng 10 2018
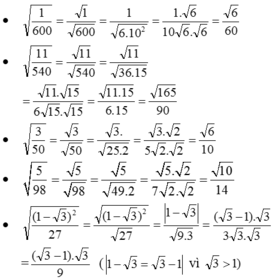
(Ghi nhớ: Khử căn ở mẫu tức là nhân cả tử và mẫu với thừa số có chứa căn.)
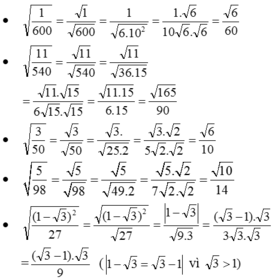
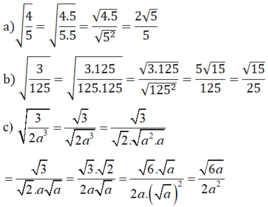
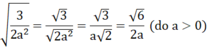
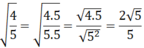
(do xy > 0 (gt) nên đưa thừa số xy vào trong căn để khử mẫu)