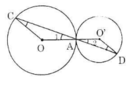
Trên hình 89, hai đường tròn tiếp xúc nhau tại A. Chứng minh rằng OC // O'D.
Hình 89
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: OA = OC (bán kính) nên ΔOAC cân tại O.
![]()
Lại có O'A = O'D (bán kính) nên ΔO'AD cân tại O'

Vậy OC // O'D (có hai góc so le trong bằng nhau).


Tam giác COA cân: ∠C = ∠A1
Tam giác DO’A cân: ∠D = ∠A2
Mà ∠A1 = ∠A2 (đối đỉnh)
⇒ ∠C = ∠D ⇒ OC//O’D

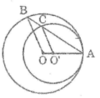
Ta có: OA = OB (= R)
Suy ra tam giác AOB cân tại O
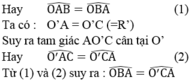
Suy ra: OB // O’C (vì có hai góc ở vị trí đồng vị bằng nhau)
Ta có: OA = OC (bán kính) nên ΔOAC cân tại O.
suy ra C ^ = O A C ^ 1
Lại có O'A = O'D (bán kính) nên ΔO'AD cân tại O'
Vậy OC // O'D (có hai góc so le trong bằng nhau).