Chiếu một tia sáng đơn sắc đến mặt bên AB của một lăng kính tiết diện là một tam giác đều ABC theo phương song song với đáy BC. Tia ló ra khỏi AC đi là là mặt AC. Chiết suất của chất làm lăng kính là:
A. 2
B. 1,8
C.1,53
D. 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A.
Chiếu một tia sáng đơn sắc tới lăng kính theo phương vuông góc với mặt phẳng bên AB ⇒ i 1 = 0 0 , r 1 = 0 0 ⇒ r 2 = 45 0 .
Tia sáng khi đi qua khỏi lăng kính nằm sát với mặt bên AC ⇒ i 2 = 90 0
Ta có: sin i 2 = n sin r 2 ⇒ n = 1 , 41.

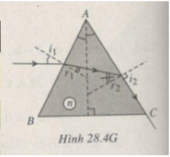
Theo đề bài: i = 30 ° ; sin r 1 = 1/2n
i 2 = 90 ° (HÌnh 28.4G); r 2 = i g h → sin r 2 = 1/n
Nhưng r 1 = A – r 2 – 60 ° - i g h
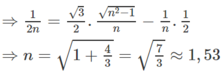

Đáp án: C
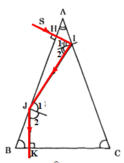
Ta có:
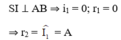
Mặt khác từ hình vẽ: SI // pháp tuyến tại J
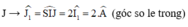
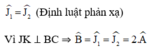
Theo tính chất góc trong của tam giác cân ABC ta có:
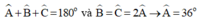

Chọn đáp án C.
n sin A = sin i ⇒ n d sin A = sin i d ⇒ 1 , 532 sin 30 0 = sin i d ⇒ i d ≈ 50 0 n t sin A = sin i t ⇒ 1 , 5867 sin 30 0 = sin i t ⇒ i t ≈ 52 , 5 0
⇒ δ = i t − i d = 2 , 5 0 .

Đáp án C
+ Tia đỏ vừa vặn phản xạ toàn phần, thì ta có thể lập luận để thấy rằng toàn bộ các tia khác cũng bị phản xạ toàn phần trên AC và khi đến BC đều ló hết ra ngoài

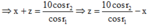
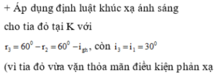
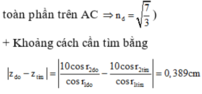
Đáp án cần chọn là: C
Vì ∆ABC là tam giác đều và tia tới đi song song với cạnh đáy BC nên dễ suy ra được i 1 = 30 0 .
Mà: sin i 1 = n sinr 1 ↔ sin 30 0 = n sinr 1 → n sinr 1 = 0,5 (1)
Tia ló đi là là mặt AC, nên i 2 = 90 0
Góc chiết quang: A = r 1 + r 2
Ta lại có:
sin i 2 = n sinr 2 ↔ sin 90 = n sin ( A − r 1 )
↔ sin 90 = n sin ( 60 − r 1 ) ( 2 )
Lấy (2) chia cho (1) ta được:
sin 90 0,5 = n sin ( 60 − r 1 ) n sinr 1 ↔ 2 s i n r 1 = s i n ( 60 − r 1 )
↔ 2 sin r 1 = sin 60 c osr 1 − c os 60 sinr 1
↔ ( 2 + c os 60 ) sinr 1 = sin 60. c osr 1
→ tanr 1 = sin 60 2 + c os 60 = 3 5 → r 1 = 19,1 0
Thay vào (1), ta được: n = 0,5 sinr 1 = 0,5 sin 19,1 0 = 1,53