Phương trình m + 1 x 2 - x - 3 m + 4 = 0 có hai nghiệm trái dấu khi và chỉ khi
A. m < - 1 hoặc m > 4 3
B. m < - 1 hoặc m > 3 4
C. m > 4 3
D. - 1 < m < 4 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Pt đã cho có 2 nghiệm trái dấu khi:
\(ac< 0\Leftrightarrow\left(m+1\right)\left(m-2\right)< 0\)
\(\Leftrightarrow-1< m< 2\)

Chọn B.
Phương trình (m + 2) x 2 - 3x + 2m - 3 = 0 có hai nghiệm trái dấu
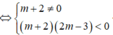
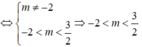
Vậy phương trình (m + 2)
x
2
- 3x + 2m - 3 = 0 có hai nghiệm trái dấu khi 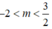

Xin lựa a;b ... c;d e rỗng tuếch :>> (ko bt đúng ko nữa).
a, Thay m = 5 vào biểu thức ta đc
\(x^2-2\left(5+6\right)x+5-4=0\)
\(x^2-33x+1=0\)
\(\Delta=\left(-33\right)^2-4.1.1=1089-4=1085>0\)
Nên phương trình có 2 nghiệm phân biệt
\(x_1=\frac{33-\sqrt{1085}}{2};x_2=\frac{33+\sqrt{1085}}{2}\)
b, Ta có :
\(\Delta=\left(2m-2\right)^2-4\left(m-4\right)=4m^2-4-4m+16=4m^2-4m+12\)
\(=\left(4m^2-4m+1\right)+11\ge11\forall m\)
Vậy phuwong trình có 2 nghiệm phân biệt vs mọi x

a: Khi m=1 thì pt sẽ là: x^2+4x-3=0
=>x=-2+căn 7 hoặc x=-2-căn 7
b: Δ=(2m-6)^2-4(m-4)
=4m^2-24m+36-4m+16
=4m^2-28m+52=(2m-7)^2+3>0
=>PT luôn có hai nghiệm pb
c: PT có hai nghiệm trái dấu
=>m-4<0
=>m<4

Phương trình có hai nghiệm trái dấu khi và chỉ khi ![]() suy ra m < -2.
suy ra m < -2.
Tổng của hai nghiệm bằng -3 khi ![]() thỏa mãn điều kiện m < -2.
thỏa mãn điều kiện m < -2.
Đáp số: m = -5.

\(x^2-2\left(m+1\right)x+m-4=0\)
( a = 1 , b = -2(m+1) , c = m - 4 )
\(\Delta=b^2-4ac\)
\(=\left[-2\left(m+1\right)\right]^2-4.1.\left(m-4\right)\)
\(=4\left(m^2+2m+1\right)-4m+16\)
\(=4m^2+8m+4-4m+16\)
\(=4m^2+4m+20\)
\(=4m^2+4m+1^2-1^2+20\)
\(=\left(2m+1\right)^2+19>0\)với mọi m
Vậy pt có 2 nghiệm pb với mọi m
Ta có: \(P=x_2.x_1=\frac{c}{a}=\frac{m-4}{1}=m-4\)
Để có 2 no cùng dấu thì \(\hept{\begin{cases}\Delta\ge0\\P>0\end{cases}}\)
\(P>0\Leftrightarrow m-4>0\Leftrightarrow m>4\)

a:Δ=(2m-2)^2-4(-m-3)
=4m^2-8m+4+4m+12
=4m^2-4m+16
=(2m-1)^2+15>=15>0
=>Phương trình luôn có hai nghiệm phân biệt
b: Để phương trình có hai nghiệm trái dấu thì -m-3<0
=>m+3>0
=>m>-3
c: Để phương trình có hai nghiệm âm thì:
2m-2<0 và -m-3>0
=>m<1 và m<-3
=>m<-3
d: x1^2+x2^2=(x1+x2)^2-2x1x2
=(2m-2)^2-2(-m-3)
=4m^2-8m+4+2m+6
=4m^2-6m+10
=4(m^2-3/2m+5/2)
=4(m^2-2*m*3/4+9/16+31/16)
=4(m-3/4)^2+31/4>0 với mọi m