Cho hình vuông ABCD có tâm O và trục (L) đi qua O. Xác định số đo của các góc giữa tia OA và trục (L), biết trục (L) đi qua đỉnh A của hình vuông.
A. 1800 + k.3600.
B. 900 + k.360.
C. -900 + k.3600.
D. k.3600.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
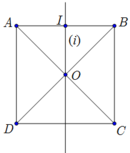
Từ hình vẽ ta có nhận xét sau:
![]() và OA= OB ( do ABCD là hình vuông có O là giao điểm của 2 đường chéo)
và OA= OB ( do ABCD là hình vuông có O là giao điểm của 2 đường chéo)
Tam giác AOB vuông cân tại O ( tính chất hình vuông)
Trục (i) đi qua trung điểm của AB nên ![]()
Suy ra trục (i) là đường phân giác của góc ![]() nên
nên 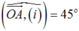 .
.

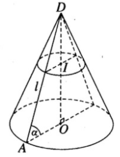
Thiết diện qua I và vuông góc với trục hình nón là một hình tròn bán kính r’
với 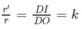
Gọi s là diện tích của thiết diện và S là diện tích của đáy hình tròn ta có:
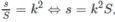
trong đó S = πr 2 = πl 2 cos 2 α
Vậy diện tích của thiết diện đi qua điểm I và vuông góc với trục hình nón là: s = k 2 s = k 2 πl 2 cos 2 α

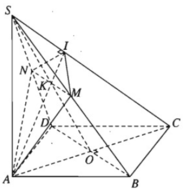
a) Gọi I là giao điểm của mặt phẳng (α) với cạnh SC. Ta có: (α) ⊥ SC, AI ⊂ (α) ⇒ SC ⊥ AI. Vậy AI là đường cao của tam giác vuông SAC. Trong mặt phẳng (SAC), đường cao AI cắt SO tại K và AI ⊂ (α), nên K là giao điểm của SO với (α).
b) Ta có 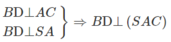
⇒ BD ⊥ SC
Mặt khác BD ⊂ (SBD) nên (SBD) ⊥ (SAC).
Vì BD ⊥ SC và (α) ⊥ SC nhưng BD không chứa trong (α) nên BD // (α)
Ta có K = SO ∩ (α) và SO thuộc mặt phẳng (SBD) nên K là một điểm chung của (α) và (SBD).
Mặt phẳng (SBD) chứa BD // (α) nên cắt theo giao tuyến d // BD. Giao tuyến này đi qua K là điểm chung của (α) và (SBD).
Gọi M và N lần lượt là giao điểm của d với SB và SD. Ta được thiết diện là tứ giác AIMN vuông góc với SC và đường chéo MN song song với BD.

Gọi tam giác A'B'C' là ảnh của tam giác ABC qua phép biến hình trên.

(e)Phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng qua trục Oy và phép vị tự tâm O tỉ số k = -2
+) Qua phép đối xứng qua trục Oy biến tam giác ABC thành tam giác A 1 B 1 C 1
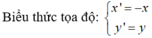
Do đó, tọa độ A 1 - 1 ; 1 ; B 1 0 ; 3 v à C 1 - 2 ; 4 .
+) Qua phép vị tự tâm O tỉ số k = -2 biến tam giác A 1 B 1 C 1 thành tam giác A 2 B 2 C 2
Biểu thức tọa độ :
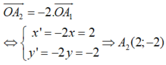
Tương tự; B 2 0 ; - 6 v à C 2 4 ; - 8
Vậy qua phép đối xứng trục Oy và phép vị tự tâm O tỉ số k = -2, biến các điểm A, B, C lần lượt thành
A 2 2 ; - 2 ; B 2 0 ; - 6 v à C 2 4 ; - 8 .

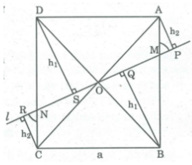
Gọi h 1 và h 2 là khoảng cách từ đỉnh B và đỉnh A đến đường thẳng l
Tổng khoảng cách là S.
Vì O là tâm đối xứng của hình vuông nên OM = ON (tính chất đối xứng tâm)
Suy ra AM = CN
Mà: ∠ (AMP) = ∠ (DNS) (đồng vị)
∠ (DNS) = ∠ (CNR) (đôi đỉnh)
Suy ra: ∠ (AMP) = ∠ (CNR)
Suy ra: ∆ APM = ∆ CRN (cạnh huyền, góc nhọn)
⇒ CR = AP = h 2
AM = CN ⇒ BM = DR
∠ (BMQ) = ∠ (DNS) (so le trong)
Suy ra: ∆ BQM = ∆ DSN (cạnh huyền, góc nhọn) ⇒ DS = BQ = h 1
S B O A = 1 / 4 S A O B = 1 / 4 a 2 (l)
S B O A = S B O M + S A O M = 1/2 .b/2 . h 1 + 1/2 .b/2 . h 2
Từ (1) và (2) suy ra h 1 + h 2 = a 2 b . Vậy : S = 2( h 1 + h 2 ) = 2 a 2 b
Chọn D.
Vì trục (L) đi qua đỉnh A và tâm O của hình vuông nên trục (L) trung với đường thẳng OA
Suy ra: số đo của các góc giữa tia OA với trục (L) bằng 00 + k.3600 = k.3600.