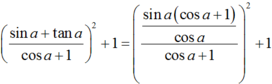Kết quả rút gọn của biểu thức sin a + tan a c o s a + 1 2 + 1 bằng
A. cos2a
B. tan2a
C. 1 cos 2 a
D. 1 sin 2 a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với a > 1, ta có
\(\dfrac{a-\sqrt{a}}{1-\sqrt{a}}=\dfrac{\sqrt{a\left(\sqrt{a-1}\right)}}{1-\sqrt{a}}\dfrac{-\sqrt{a\left(1-\sqrt{a}\right)}}{1-\sqrt{a}}=\sqrt{a}\)
banjcho mình hỏi bài này là làm theo cách nào thê, mong bạn chỉ mình, mình cảm mơn



\(\cos \left( {a + b} \right)\cos \left( {a - b} \right) - \sin \left( {a + b} \right)\sin \left( {a - b} \right)\)
\( = \frac{1}{2}\left[ {\cos \left( {a + b - a + b} \right) + \cos \left( {a + b + a - b} \right)} \right] - \frac{1}{2}\left[ {\cos \left( {a + b - a + b} \right) - \cos \left( {a + b + a - b} \right)} \right]\)
\( = \frac{1}{2}\left( {\cos 2b + \cos 2a - \cos 2b + \cos 2a} \right) = \frac{1}{2}.2\cos 2a = \cos 2a = 1 - 2{\sin ^2}a\)
Vậy chọn đáp án C
Chọn C.
Ta có